Example-01: Coupled twiss parameters
[1]:
import torch
torch.set_printoptions(precision=3, sci_mode=True)
[2]:
# Set elements
def drif(x, l):
(qx, px, qy, py), l = x, l
return torch.stack([qx + l*px, px, qy + l*py, py])
def quad(x, kn, ks, l, n=25):
(qx, px, qy, py), kn, ks, l = x, kn, ks, l/(2.0*n)
for _ in range(n):
qx, qy = qx + l*px, qy + l*py
px, py = px - 2.0*l*(kn*qx - ks*qy), py + 2.0*l*(ks*qx + kn*qy)
qx, qy = qx + l*px, qy + l*py
return torch.stack([qx, px, qy, py])
[3]:
# Set transport maps
def m11(x, k): kn1, ks1, kn2, ks2 = k; return x
def m12(x, k): kn1, ks1, kn2, ks2 = k; x = quad(x, kn1, ks1, 0.5); return x
def m23(x, k): kn1, ks1, kn2, ks2 = k; x = drif(x, 2.5); return x
def m34(x, k): kn1, ks1, kn2, ks2 = k; x = drif(x, 2.5); return x
def m45(x, k): kn1, ks1, kn2, ks2 = k; x = quad(x, kn2, ks2, 0.5); return x
def m56(x, k): kn1, ks1, kn2, ks2 = k; x = quad(x, kn2, ks2, 0.5); return x
def m67(x, k): kn1, ks1, kn2, ks2 = k; x = drif(x, 2.5); return x
def m78(x, k): kn1, ks1, kn2, ks2 = k; x = drif(x, 2.5); return x
def m89(x, k): kn1, ks1, kn2, ks2 = k; x = quad(x, kn1, ks1, 0.5); return x
[4]:
# Set fodo cell
def fodo(x, k):
x = m11(x, k)
x = m12(x, k)
x = m23(x, k)
x = m34(x, k)
x = m45(x, k)
x = m56(x, k)
x = m67(x, k)
x = m78(x, k)
x = m89(x, k)
return x
[5]:
# Compute one-turn transport matrix
x = torch.tensor([0.0, 0.0, 0.0, 0.0], dtype=torch.float64)
k = torch.tensor([0.20, -0.01, -0.25, 0.01], dtype=torch.float64)
m = torch.func.jacrev(fodo)(x, k)
print(m)
from twiss import is_stable
print(is_stable(m))
tensor([[ 4.946e-01, 2.032e+01, -8.454e-03, 3.297e-01],
[-3.725e-02, 4.946e-01, 4.386e-03, 8.052e-03],
[ 8.052e-03, 3.297e-01, -9.236e-02, 3.539e+00],
[ 4.386e-03, -8.454e-03, -2.806e-01, -9.236e-02]], dtype=torch.float64)
True
[6]:
# Compute coupled twiss parameters
from twiss import twiss
t, n, w = twiss(m)
print(t)
print(n)
print(w)
tensor([1.677e-01, 2.647e-01], dtype=torch.float64)
tensor([[ 4.835e+00, 0.000e+00, 2.714e-02, -2.788e-16],
[-3.407e-17, 2.069e-01, 6.135e-18, -7.283e-03],
[ 6.634e-02, 3.851e-17, 1.884e+00, 0.000e+00],
[-1.459e-17, -2.980e-03, 1.841e-16, 5.308e-01]], dtype=torch.float64)
tensor([[[ 2.338e+01, -1.647e-16, 3.208e-01, -7.055e-17],
[-1.647e-16, 4.279e-02, 5.706e-18, -6.165e-04],
[ 3.208e-01, 5.706e-18, 4.401e-03, -1.083e-18],
[-7.055e-17, -6.165e-04, -1.083e-18, 8.880e-06]],
[[ 7.367e-04, 2.197e-18, 5.114e-02, -1.430e-16],
[ 2.197e-18, 5.305e-05, 1.156e-17, -3.866e-03],
[ 5.114e-02, 1.156e-17, 3.550e+00, 3.469e-16],
[-1.430e-16, -3.866e-03, 3.469e-16, 2.818e-01]]],
dtype=torch.float64)
[7]:
# Check normalization matrix
from math import pi
from twiss import rotation
print(rotation(*2*pi*t))
print(n.inverse() @ m @ n)
tensor([[4.945e-01, 8.692e-01, 0.000e+00, 0.000e+00],
[-8.692e-01, 4.945e-01, 0.000e+00, 0.000e+00],
[0.000e+00, 0.000e+00, -9.224e-02, 9.957e-01],
[0.000e+00, 0.000e+00, -9.957e-01, -9.224e-02]], dtype=torch.float64)
tensor([[ 4.945e-01, 8.692e-01, -4.585e-18, 5.551e-17],
[-8.692e-01, 4.945e-01, 8.179e-17, -3.221e-17],
[ 9.636e-18, 9.741e-18, -9.224e-02, 9.957e-01],
[ 1.133e-17, -2.888e-17, -9.957e-01, -9.224e-02]], dtype=torch.float64)
[8]:
# Check twiss matrices
from twiss.matrix import symplectic_identity
s = symplectic_identity(len(w), dtype=torch.float64)
u = torch.zeros_like(m)
for ti, wi in zip(t, w):
u += (wi @ s) * (2*pi*ti).sin() - (wi @ s) @ (wi @ s) * (2*pi*ti).cos()
print(m)
print(u)
tensor([[ 4.946e-01, 2.032e+01, -8.454e-03, 3.297e-01],
[-3.725e-02, 4.946e-01, 4.386e-03, 8.052e-03],
[ 8.052e-03, 3.297e-01, -9.236e-02, 3.539e+00],
[ 4.386e-03, -8.454e-03, -2.806e-01, -9.236e-02]], dtype=torch.float64)
tensor([[ 4.946e-01, 2.032e+01, -8.454e-03, 3.297e-01],
[-3.725e-02, 4.946e-01, 4.386e-03, 8.052e-03],
[ 8.052e-03, 3.297e-01, -9.236e-02, 3.539e+00],
[ 4.386e-03, -8.454e-03, -2.806e-01, -9.236e-02]], dtype=torch.float64)
[9]:
# Compute twiss at each location
from twiss import propagate
out = []
for mapping in (m11, m12, m23, m34, m45, m56, m67, m78, m89):
w = propagate(w, torch.func.jacrev(mapping)(x, k))
out.append(w)
out = torch.stack(out)
print(out.shape)
torch.Size([9, 2, 4, 4])
[10]:
# Convert to CS and LB represencation
from twiss import wolski_to_cs
from twiss import wolski_to_lb
ax, bx, ay, by = torch.vmap(wolski_to_cs)(out).T
a1x, b1x, a2x, b2x, a1y, b1y, a2y, b2y, *_ = torch.vmap(wolski_to_lb)(out).T
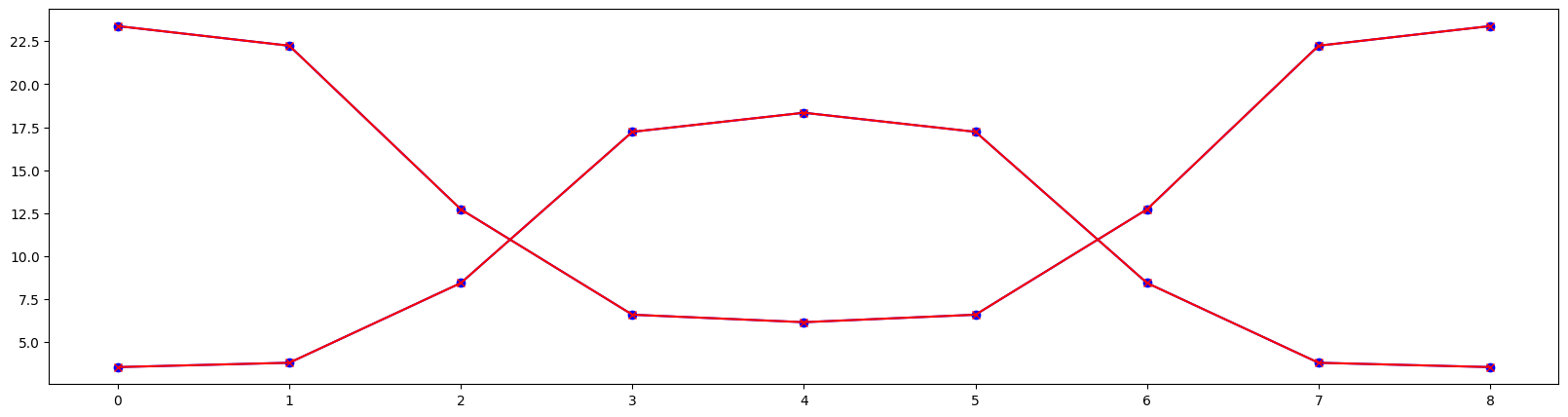
[11]:
# Plot in-plane twiss parameters
from matplotlib import pyplot as plt
plt.figure(figsize=(20, 5))
plt.plot(range(9), bx, marker='o', color='blue')
plt.plot(range(9), b1x, marker='x', color='red')
plt.plot(range(9), by, marker='o', color='blue')
plt.plot(range(9), b2y, marker='x', color='red')
plt.show()
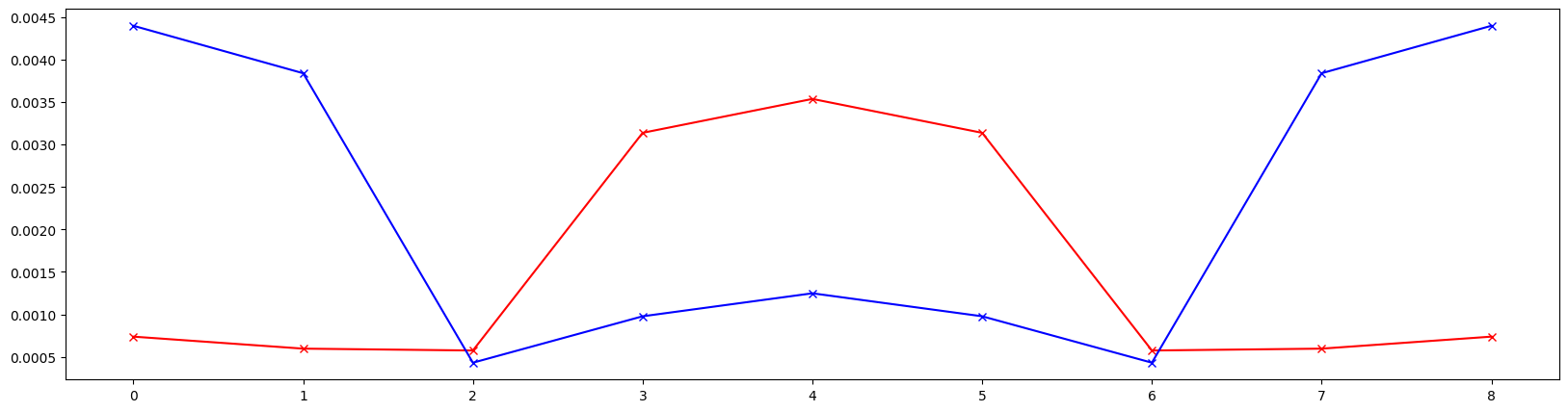
[12]:
# Plot in-plane coupled twiss parameters
from matplotlib import pyplot as plt
plt.figure(figsize=(20, 5))
plt.plot(range(9), b2x, marker='x', color='red')
plt.plot(range(9), b1y, marker='x', color='blue')
plt.show()
[13]:
# Compute phase advances
from twiss import advance
out = []
for mapping in (m11, m12, m23, m34, m45, m56, m67, m78, m89):
mu, n = advance(n, torch.func.jacrev(mapping)(x, k))
out.append(mu)
out = torch.stack(out)
print(t)
print(1/(2*pi)*out.T.sum(-1))
tensor([1.677e-01, 2.647e-01], dtype=torch.float64)
tensor([1.677e-01, 2.647e-01], dtype=torch.float64)
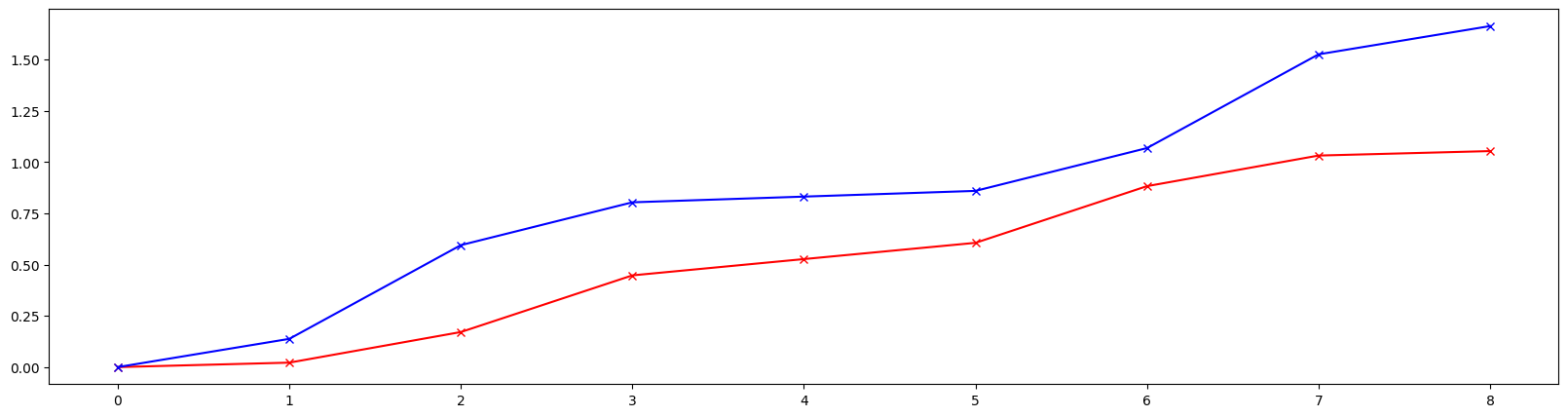
[14]:
# Plot accumulated phase advance
mux, muy = out.T.cumsum(-1)
plt.figure(figsize=(20, 5))
plt.plot(range(9), mux, marker='x', color='red')
plt.plot(range(9), muy, marker='x', color='blue')
plt.show()
Example-02: Tune derivatives
[1]:
import torch
torch.set_printoptions(precision=3, sci_mode=True)
[2]:
# Set elements
def drif(x, l):
(qx, px, qy, py), l = x, l
return torch.stack([qx + l*px, px, qy + l*py, py])
def quad(x, kn, ks, l, n=25):
(qx, px, qy, py), kn, ks, l = x, kn, ks, l/(2.0*n)
for _ in range(n):
qx, qy = qx + l*px, qy + l*py
px, py = px - 2.0*l*(kn*qx - ks*qy), py + 2.0*l*(ks*qx + kn*qy)
qx, qy = qx + l*px, qy + l*py
return torch.stack([qx, px, qy, py])
[3]:
# Set transport maps
def m11(x, k): kn1, ks1, kn2, ks2 = k; return x
def m12(x, k): kn1, ks1, kn2, ks2 = k; x = quad(x, kn1, ks1, 0.5); return x
def m23(x, k): kn1, ks1, kn2, ks2 = k; x = drif(x, 2.5); return x
def m34(x, k): kn1, ks1, kn2, ks2 = k; x = drif(x, 2.5); return x
def m45(x, k): kn1, ks1, kn2, ks2 = k; x = quad(x, kn2, ks2, 0.5); return x
def m56(x, k): kn1, ks1, kn2, ks2 = k; x = quad(x, kn2, ks2, 0.5); return x
def m67(x, k): kn1, ks1, kn2, ks2 = k; x = drif(x, 2.5); return x
def m78(x, k): kn1, ks1, kn2, ks2 = k; x = drif(x, 2.5); return x
def m89(x, k): kn1, ks1, kn2, ks2 = k; x = quad(x, kn1, ks1, 0.5); return x
[4]:
# Set fodo cell
def fodo(x, k):
x = m11(x, k)
x = m12(x, k)
x = m23(x, k)
x = m34(x, k)
x = m45(x, k)
x = m56(x, k)
x = m67(x, k)
x = m78(x, k)
x = m89(x, k)
return x
[5]:
# Compute tune derivatives
from twiss import twiss
x = torch.tensor([0.0, 0.0, 0.0, 0.0], dtype=torch.float64)
k = torch.tensor([0.20, 0.0, -0.25, 0.0], dtype=torch.float64)
def fn(k):
m = torch.func.jacrev(fodo)(x, k)
t, *_ = twiss(m)
return t
d1 = torch.func.jacrev(fn)(k)
d2 = torch.func.jacrev(torch.func.jacrev(fn))(k)
print(d1)
print(d2)
tensor([[1.832e+00, 0.000e+00, 5.027e-01, 0.000e+00],
[-2.894e-01, 0.000e+00, -1.430e+00, 0.000e+00]], dtype=torch.float64)
tensor([[[-1.265e+01, 0.000e+00, -6.634e+00, 0.000e+00],
[0.000e+00, -1.186e+01, 0.000e+00, -1.682e+01],
[-6.634e+00, 0.000e+00, -1.069e+00, 0.000e+00],
[0.000e+00, -1.682e+01, 0.000e+00, -1.547e+01]],
[[-4.998e-02, 0.000e+00, -2.576e+00, 0.000e+00],
[0.000e+00, 9.716e+00, 0.000e+00, 8.931e+00],
[-2.576e+00, 0.000e+00, 7.011e-01, 0.000e+00],
[0.000e+00, 8.931e+00, 0.000e+00, 1.286e+01]]], dtype=torch.float64)
[6]:
# Test
dk = torch.tensor([0.005, -0.005, -0.005, 0.005], dtype=torch.float64)
print(fn(k))
print(fn(k) + d1 @ dk)
print(fn(k) + d1 @ dk + 1/2 * d2 @ dk @ dk)
print()
t, *_ = twiss(torch.func.jacrev(fodo)(x, k + dk))
print(t)
print()
tensor([1.674e-01, 2.645e-01], dtype=torch.float64)
tensor([1.740e-01, 2.702e-01], dtype=torch.float64)
tensor([1.741e-01, 2.703e-01], dtype=torch.float64)
tensor([1.741e-01, 2.703e-01], dtype=torch.float64)
Example-03: Twiss derivatives
[1]:
import torch
torch.set_printoptions(precision=3, sci_mode=True)
[2]:
# Set elements
def drif(x, l):
(qx, px, qy, py), l = x, l
return torch.stack([qx + l*px, px, qy + l*py, py])
def quad(x, kn, ks, l, n=25):
(qx, px, qy, py), kn, ks, l = x, kn, ks, l/(2.0*n)
for _ in range(n):
qx, qy = qx + l*px, qy + l*py
px, py = px - 2.0*l*(kn*qx - ks*qy), py + 2.0*l*(ks*qx + kn*qy)
qx, qy = qx + l*px, qy + l*py
return torch.stack([qx, px, qy, py])
[3]:
# Set transport maps
def m11(x, k): kn1, ks1, kn2, ks2 = k; return x
def m12(x, k): kn1, ks1, kn2, ks2 = k; x = quad(x, kn1, ks1, 0.5); return x
def m23(x, k): kn1, ks1, kn2, ks2 = k; x = drif(x, 2.5); return x
def m34(x, k): kn1, ks1, kn2, ks2 = k; x = drif(x, 2.5); return x
def m45(x, k): kn1, ks1, kn2, ks2 = k; x = quad(x, kn2, ks2, 0.5); return x
def m56(x, k): kn1, ks1, kn2, ks2 = k; x = quad(x, kn2, ks2, 0.5); return x
def m67(x, k): kn1, ks1, kn2, ks2 = k; x = drif(x, 2.5); return x
def m78(x, k): kn1, ks1, kn2, ks2 = k; x = drif(x, 2.5); return x
def m89(x, k): kn1, ks1, kn2, ks2 = k; x = quad(x, kn1, ks1, 0.5); return x
[4]:
# Set fodo cell
def fodo(x, k):
x = m11(x, k)
x = m12(x, k)
x = m23(x, k)
x = m34(x, k)
x = m45(x, k)
x = m56(x, k)
x = m67(x, k)
x = m78(x, k)
x = m89(x, k)
return x
[5]:
# Set task function
from twiss import twiss
from twiss import propagate
from twiss import wolski_to_cs
x = torch.tensor([0.0, 0.0, 0.0, 0.0], dtype=torch.float64)
k = torch.tensor([0.20, 0.0, -0.25, 0.0], dtype=torch.float64)
def fn(k):
m = torch.func.jacrev(fodo)(x, k)
*_, w = twiss(m)
out = []
for mapping in (m11, m12, m23, m34, m45, m56, m67, m78, m89):
w = propagate(w, torch.func.jacrev(mapping)(x, k))
out.append(w)
out = torch.stack(out)
ax, bx, ay, by = torch.vmap(wolski_to_cs)(out).T
return torch.stack([bx, by]).T
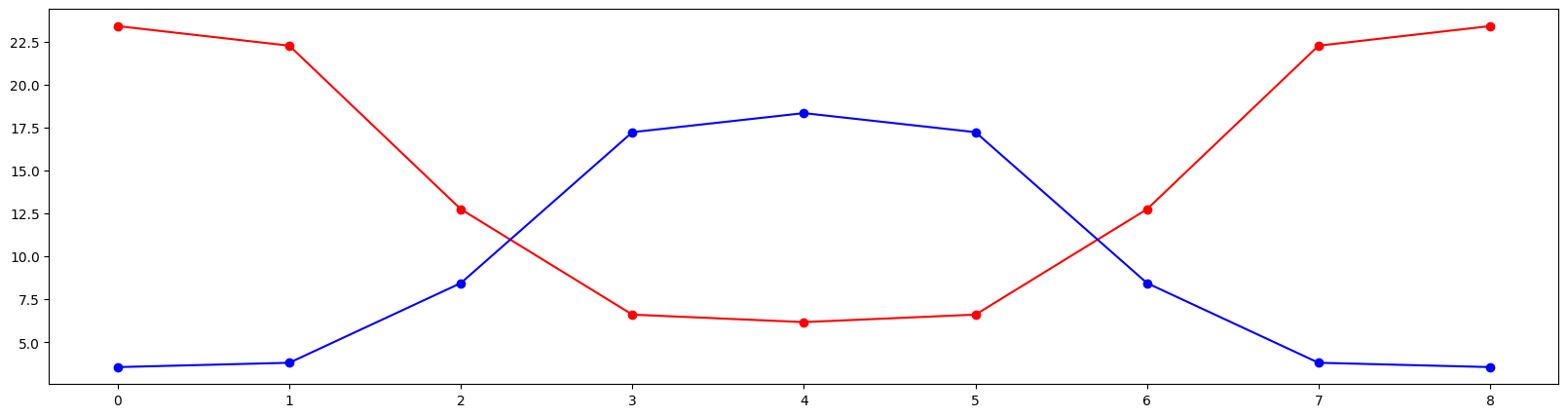
[6]:
# Compute and plot twiss
bx, by = fn(k).T
from matplotlib import pyplot as plt
plt.figure(figsize=(20, 5))
plt.plot(range(9), bx, marker='o', color='red')
plt.plot(range(9), by, marker='o', color='blue')
plt.show()
[7]:
# Compute twiss derivatives
d1 = torch.func.jacrev(fn)(k)
print(d1.shape)
torch.Size([9, 2, 4])
[8]:
# Test
dk = torch.tensor([0.005, -0.005, -0.005, 0.005], dtype=torch.float64)
print(fn(k).T)
print((fn(k) + d1 @ dk).T)
print()
print(fn(k + dk).T)
print()
tensor([[2.341e+01, 2.226e+01, 1.274e+01, 6.608e+00, 6.173e+00, 6.608e+00, 1.274e+01, 2.226e+01, 2.341e+01],
[3.554e+00, 3.806e+00, 8.444e+00, 1.723e+01, 1.834e+01, 1.723e+01, 8.444e+00, 3.806e+00, 3.554e+00]],
dtype=torch.float64)
tensor([[2.303e+01, 2.188e+01, 1.232e+01, 6.251e+00, 5.827e+00, 6.251e+00, 1.232e+01, 2.188e+01, 2.303e+01],
[3.395e+00, 3.647e+00, 8.370e+00, 1.741e+01, 1.856e+01, 1.741e+01, 8.370e+00, 3.647e+00, 3.395e+00]],
dtype=torch.float64)
tensor([[2.305e+01, 2.190e+01, 1.234e+01, 6.262e+00, 5.838e+00, 6.262e+00, 1.234e+01, 2.190e+01, 2.305e+01],
[3.396e+00, 3.648e+00, 8.373e+00, 1.742e+01, 1.857e+01, 1.742e+01, 8.373e+00, 3.648e+00, 3.396e+00]],
dtype=torch.float64)
Example-04: Phase advance derivatives
[1]:
import torch
torch.set_printoptions(precision=3, sci_mode=True)
[2]:
# Set elements
def drif(x, l):
(qx, px, qy, py), l = x, l
return torch.stack([qx + l*px, px, qy + l*py, py])
def quad(x, kn, ks, l, n=25):
(qx, px, qy, py), kn, ks, l = x, kn, ks, l/(2.0*n)
for _ in range(n):
qx, qy = qx + l*px, qy + l*py
px, py = px - 2.0*l*(kn*qx - ks*qy), py + 2.0*l*(ks*qx + kn*qy)
qx, qy = qx + l*px, qy + l*py
return torch.stack([qx, px, qy, py])
[3]:
# Set transport maps
def m11(x, k): kn1, ks1, kn2, ks2 = k; return x
def m12(x, k): kn1, ks1, kn2, ks2 = k; x = quad(x, kn1, ks1, 0.5); return x
def m23(x, k): kn1, ks1, kn2, ks2 = k; x = drif(x, 2.5); return x
def m34(x, k): kn1, ks1, kn2, ks2 = k; x = drif(x, 2.5); return x
def m45(x, k): kn1, ks1, kn2, ks2 = k; x = quad(x, kn2, ks2, 0.5); return x
def m56(x, k): kn1, ks1, kn2, ks2 = k; x = quad(x, kn2, ks2, 0.5); return x
def m67(x, k): kn1, ks1, kn2, ks2 = k; x = drif(x, 2.5); return x
def m78(x, k): kn1, ks1, kn2, ks2 = k; x = drif(x, 2.5); return x
def m89(x, k): kn1, ks1, kn2, ks2 = k; x = quad(x, kn1, ks1, 0.5); return x
[4]:
# Set fodo cell
def fodo(x, k):
x = m11(x, k)
x = m12(x, k)
x = m23(x, k)
x = m34(x, k)
x = m45(x, k)
x = m56(x, k)
x = m67(x, k)
x = m78(x, k)
x = m89(x, k)
return x
[5]:
# Set task function
from twiss import twiss
from twiss import advance
x = torch.tensor([0.0, 0.0, 0.0, 0.0], dtype=torch.float64)
k = torch.tensor([0.20, 0.0, -0.25, 0.0], dtype=torch.float64)
def fn(k):
m = torch.func.jacrev(fodo)(x, k)
_, n, _ = twiss(m)
out = []
for mapping in (m12, m23, m34, m45, m56, m67, m78, m89):
mu, n = advance(n, torch.func.jacrev(mapping)(x, k))
out.append(mu)
return torch.stack(out)
[6]:
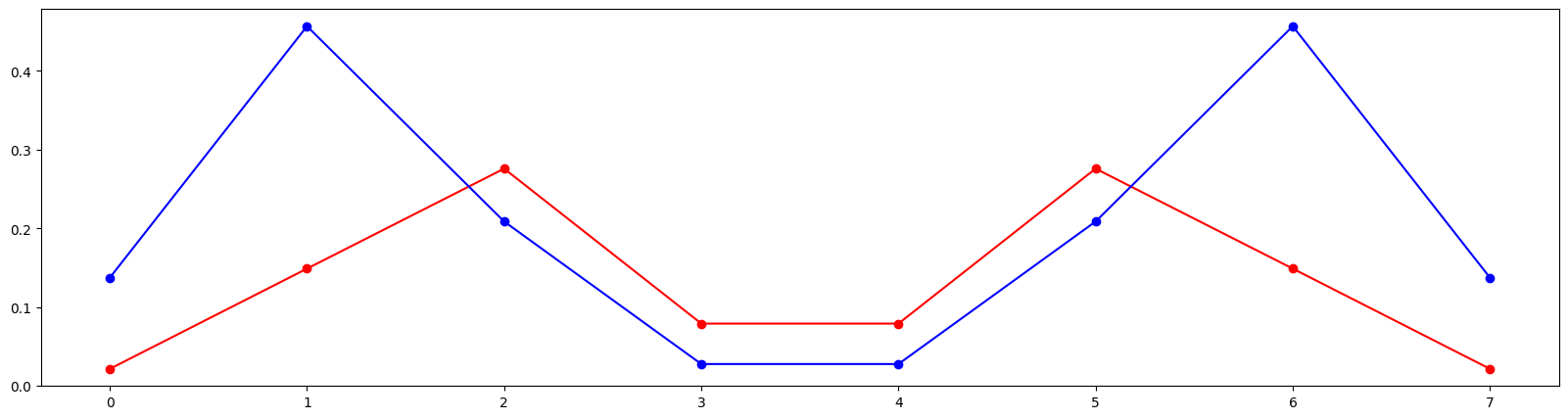
# Compute and plot phase advance
mux, muy = fn(k).T
from matplotlib import pyplot as plt
plt.figure(figsize=(20, 5))
plt.plot(range(8), mux, marker='o', color='red')
plt.plot(range(8), muy, marker='o', color='blue')
plt.show()
[7]:
# Compute phase advance derivatives
d1 = torch.func.jacrev(fn)(k)
print(d1.shape)
torch.Size([8, 2, 4])
[8]:
# Test
dk = torch.tensor([0.005, -0.005, -0.005, 0.005], dtype=torch.float64)
print(fn(k).T)
print((fn(k) + d1 @ dk).T)
print()
print(fn(k + dk).T)
print()
tensor([[2.172e-02, 1.490e-01, 2.759e-01, 7.918e-02, 7.918e-02, 2.759e-01, 1.490e-01, 2.172e-02],
[1.375e-01, 4.567e-01, 2.088e-01, 2.784e-02, 2.784e-02, 2.088e-01, 4.567e-01, 1.375e-01]],
dtype=torch.float64)
tensor([[2.208e-02, 1.528e-01, 2.883e-01, 8.357e-02, 8.357e-02, 2.883e-01, 1.528e-01, 2.208e-02],
[1.435e-01, 4.691e-01, 2.086e-01, 2.752e-02, 2.752e-02, 2.086e-01, 4.691e-01, 1.435e-01]],
dtype=torch.float64)
tensor([[2.206e-02, 1.527e-01, 2.884e-01, 8.368e-02, 8.368e-02, 2.884e-01, 1.527e-01, 2.206e-02],
[1.438e-01, 4.694e-01, 2.085e-01, 2.751e-02, 2.751e-02, 2.085e-01, 4.694e-01, 1.438e-01]],
dtype=torch.float64)
Example-05: Tune uncertainty from systematic errors
[1]:
import torch
torch.set_printoptions(precision=3, sci_mode=True)
[2]:
# Set elements
def drif(x, l):
(qx, px, qy, py), l = x, l
return torch.stack([qx + l*px, px, qy + l*py, py])
def quad(x, kn, ks, l, n=25):
(qx, px, qy, py), kn, ks, l = x, kn, ks, l/(2.0*n)
for _ in range(n):
qx, qy = qx + l*px, qy + l*py
px, py = px - 2.0*l*(kn*qx - ks*qy), py + 2.0*l*(ks*qx + kn*qy)
qx, qy = qx + l*px, qy + l*py
return torch.stack([qx, px, qy, py])
[3]:
# Set transport maps
def m11(x, k): kn1, ks1, kn2, ks2 = k; return x
def m12(x, k): kn1, ks1, kn2, ks2 = k; x = quad(x, kn1, ks1, 0.5); return x
def m23(x, k): kn1, ks1, kn2, ks2 = k; x = drif(x, 2.5); return x
def m34(x, k): kn1, ks1, kn2, ks2 = k; x = drif(x, 2.5); return x
def m45(x, k): kn1, ks1, kn2, ks2 = k; x = quad(x, kn2, ks2, 0.5); return x
def m56(x, k): kn1, ks1, kn2, ks2 = k; x = quad(x, kn2, ks2, 0.5); return x
def m67(x, k): kn1, ks1, kn2, ks2 = k; x = drif(x, 2.5); return x
def m78(x, k): kn1, ks1, kn2, ks2 = k; x = drif(x, 2.5); return x
def m89(x, k): kn1, ks1, kn2, ks2 = k; x = quad(x, kn1, ks1, 0.5); return x
[4]:
# Set fodo cell
def fodo(x, k):
x = m11(x, k)
x = m12(x, k)
x = m23(x, k)
x = m34(x, k)
x = m45(x, k)
x = m56(x, k)
x = m67(x, k)
x = m78(x, k)
x = m89(x, k)
return x
[5]:
# Compute tune derivatives
from twiss import twiss
x = torch.tensor([0.0, 0.0, 0.0, 0.0], dtype=torch.float64)
k = torch.tensor([0.20, 0.0, -0.25, 0.0], dtype=torch.float64)
def fn(k):
m = torch.func.jacrev(fodo)(x, k)
t, *_ = twiss(m)
return t
grad = torch.func.jacrev(fn)(k)
[6]:
# Compute tune uncertainty for given known knobs uncertanties
sk = torch.tensor([0.01, 0.005, 0.01, 0.005], dtype=torch.float64)
st = (grad**2 @ sk**2).sqrt()
print(st)
st = torch.func.vmap(fn)(k + sk * torch.randn((1024, 4), dtype=torch.float64)).T.std(-1)
print(st)
tensor([1.900e-02, 1.459e-02], dtype=torch.float64)
tensor([1.940e-02, 1.358e-02], dtype=torch.float64)
Example-06: Matching (composable)
[1]:
import torch
torch.set_printoptions(precision=3, sci_mode=True)
[2]:
# Set elements
def drif(x, l):
(qx, px, qy, py), l = x, l
return torch.stack([qx + l*px, px, qy + l*py, py])
def quad(x, kn, ks, l, n=25):
(qx, px, qy, py), kn, ks, l = x, kn, ks, l/(2.0*n)
for _ in range(n):
qx, qy = qx + l*px, qy + l*py
px, py = px - 2.0*l*(kn*qx - ks*qy), py + 2.0*l*(ks*qx + kn*qy)
qx, qy = qx + l*px, qy + l*py
return torch.stack([qx, px, qy, py])
[3]:
# Set transport maps
def m11(x, k): kn1, kn2 = k; return x
def m12(x, k): kn1, kn2 = k; x = quad(x, kn1, 0.0, 0.5); return x
def m23(x, k): kn1, kn2 = k; x = drif(x, 2.5); return x
def m34(x, k): kn1, kn2 = k; x = drif(x, 2.5); return x
def m45(x, k): kn1, kn2 = k; x = quad(x, kn2, 0.0, 0.5); return x
def m56(x, k): kn1, kn2 = k; x = quad(x, kn2, 0.0, 0.5); return x
def m67(x, k): kn1, kn2 = k; x = drif(x, 2.5); return x
def m78(x, k): kn1, kn2 = k; x = drif(x, 2.5); return x
def m89(x, k): kn1, kn2 = k; x = quad(x, kn1, 0.0, 0.5); return x
[4]:
# Set fodo cell
def fodo(x, k):
x = m11(x, k)
x = m12(x, k)
x = m23(x, k)
x = m34(x, k)
x = m45(x, k)
x = m56(x, k)
x = m67(x, k)
x = m78(x, k)
x = m89(x, k)
return x
[5]:
# Set objective function (bx & by at focusing quadrupole center)
from twiss import twiss
from twiss import wolski_to_cs
x = torch.tensor([0.0, 0.0, 0.0, 0.0], dtype=torch.float64)
k = torch.tensor([+0.20, -0.20], dtype=torch.float64)
BX, BY = torch.tensor([25.0, 5.0], dtype=torch.float64)
bag = []
def objective(k, flag=False):
m = torch.func.jacrev(fodo)(x, k)
*_, w = twiss(m)
ax, bx, ay, by = wolski_to_cs(w)
if flag:
bag.append(torch.stack([bx, by]))
return (bx - BX)**2 + (by - BY)**2
[6]:
# Set optimizer
def adam(objective, knobs, count=1, lr=0.005, betas=(0.900, 0.999), epsilon=1.0E-9):
b1, b2 = betas
history_knobs = []
history_value = []
m1 = torch.zeros_like(knobs)
m2 = torch.zeros_like(knobs)
for i in range(count):
grad = torch.func.jacrev(objective)(knobs)
m1 = b1 * m1 + (1.0 - b1) * grad
m2 = b2 * m2 + (1.0 - b2) * grad ** 2
f1 = 1/(1 - b1 ** (i + 1))
f2 = 1/(1 - b2 ** (i + 1))
knobs = knobs - lr * m1 / f1 / (torch.sqrt(m2 / f2) + epsilon)
value = objective(knobs, flag=True)
history_knobs.append(knobs)
history_value.append(value)
return tuple(map(torch.stack, [history_knobs, history_value]))
[7]:
# Optimize
knobs, value = adam(objective, k, count=128, lr=0.001)
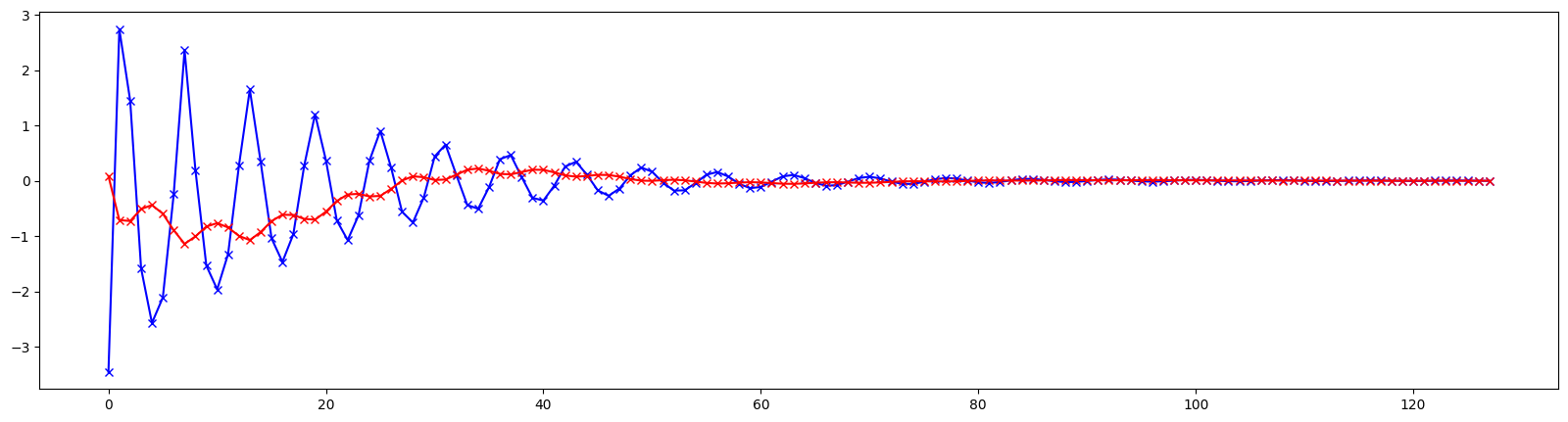
[8]:
# Plot beta values
from matplotlib import pyplot as plt
bxs, bys = torch.stack(bag).T
plt.figure(figsize=(20, 5))
plt.plot(range(128), (bxs - BX).cpu().numpy(), color='blue', marker='x')
plt.plot(range(128), (bys - BY).cpu().numpy(), color='red', marker='x')
plt.show()
Example-07: Matching (autograd)
[1]:
import torch
torch.set_printoptions(precision=3, sci_mode=True)
[2]:
# Set elements
def drif(x, l):
(qx, px, qy, py), l = x, l
return torch.stack([qx + l*px, px, qy + l*py, py])
def quad(x, kn, ks, l, n=25):
(qx, px, qy, py), kn, ks, l = x, kn, ks, l/(2.0*n)
for _ in range(n):
qx, qy = qx + l*px, qy + l*py
px, py = px - 2.0*l*(kn*qx - ks*qy), py + 2.0*l*(ks*qx + kn*qy)
qx, qy = qx + l*px, qy + l*py
return torch.stack([qx, px, qy, py])
[3]:
# Set transport maps
def m11(x, k): kn1, kn2 = k; return x
def m12(x, k): kn1, kn2 = k; x = quad(x, kn1, 0.0, 0.5); return x
def m23(x, k): kn1, kn2 = k; x = drif(x, 2.5); return x
def m34(x, k): kn1, kn2 = k; x = drif(x, 2.5); return x
def m45(x, k): kn1, kn2 = k; x = quad(x, kn2, 0.0, 0.5); return x
def m56(x, k): kn1, kn2 = k; x = quad(x, kn2, 0.0, 0.5); return x
def m67(x, k): kn1, kn2 = k; x = drif(x, 2.5); return x
def m78(x, k): kn1, kn2 = k; x = drif(x, 2.5); return x
def m89(x, k): kn1, kn2 = k; x = quad(x, kn1, 0.0, 0.5); return x
[4]:
# Set fodo cell
def fodo(x, k):
x = m11(x, k)
x = m12(x, k)
x = m23(x, k)
x = m34(x, k)
x = m45(x, k)
x = m56(x, k)
x = m67(x, k)
x = m78(x, k)
x = m89(x, k)
return x
[5]:
# Set objective function (bx & by at focusing quadrupole center)
from twiss import twiss
from twiss import wolski_to_cs
x = torch.tensor([0.0, 0.0, 0.0, 0.0], dtype=torch.float64)
k = torch.tensor([+0.20, -0.20], dtype=torch.float64)
BX, BY = torch.tensor([25.0, 5.0], dtype=torch.float64)
def objective(k):
m = torch.func.jacrev(fodo)(x, k)
*_, w = twiss(m)
ax, bx, ay, by = wolski_to_cs(w)
return (bx - BX)**2 + (by - BY)**2
[6]:
# Define model
class Model(torch.nn.Module):
def __init__(self, objective, knobs):
super().__init__()
self.objective = objective
self.knobs = torch.nn.Parameter(torch.clone(knobs))
def forward(self):
return self.objective(self.knobs)
model = Model(objective, k)
[7]:
# Set optimizer
optimizer = torch.optim.Adam(model.parameters(), lr=0.005)
[8]:
# Train
# Note, here forward method is a loss function
model.train()
for _ in range(256):
loss = model()
loss.backward()
optimizer.step()
optimizer.zero_grad()
[9]:
# Check result
k = torch.stack([*model.parameters()]).detach().squeeze()
m = torch.func.jacrev(fodo)(x, k)
*_, w = twiss(m)
ax, bx, ay, by = wolski_to_cs(w)
print(torch.stack([bx, by]))
tensor([2.500e+01, 5.000e+00], dtype=torch.float64)
Example-08: Matching (autograd & taylor model)
[1]:
import torch
torch.set_printoptions(precision=3, sci_mode=True)
[2]:
# Set elements
def drif(x, l):
(qx, px, qy, py), l = x, l
return torch.stack([qx + l*px, px, qy + l*py, py])
def quad(x, kn, ks, l, n=25):
(qx, px, qy, py), kn, ks, l = x, kn, ks, l/(2.0*n)
for _ in range(n):
qx, qy = qx + l*px, qy + l*py
px, py = px - 2.0*l*(kn*qx - ks*qy), py + 2.0*l*(ks*qx + kn*qy)
qx, qy = qx + l*px, qy + l*py
return torch.stack([qx, px, qy, py])
[3]:
# Set transport maps
def m11(x, k): kn1, kn2 = k; return x
def m12(x, k): kn1, kn2 = k; x = quad(x, kn1, 0.0, 0.5); return x
def m23(x, k): kn1, kn2 = k; x = drif(x, 2.5); return x
def m34(x, k): kn1, kn2 = k; x = drif(x, 2.5); return x
def m45(x, k): kn1, kn2 = k; x = quad(x, kn2, 0.0, 0.5); return x
def m56(x, k): kn1, kn2 = k; x = quad(x, kn2, 0.0, 0.5); return x
def m67(x, k): kn1, kn2 = k; x = drif(x, 2.5); return x
def m78(x, k): kn1, kn2 = k; x = drif(x, 2.5); return x
def m89(x, k): kn1, kn2 = k; x = quad(x, kn1, 0.0, 0.5); return x
[4]:
# Set fodo cell
def fodo(x, k):
x = m11(x, k)
x = m12(x, k)
x = m23(x, k)
x = m34(x, k)
x = m45(x, k)
x = m56(x, k)
x = m67(x, k)
x = m78(x, k)
x = m89(x, k)
return x
[5]:
# Compute parametric transport matrix
from ndmap.derivative import derivative
from ndmap.evaluate import evaluate
x = torch.tensor([0.0, 0.0, 0.0, 0.0], dtype=torch.float64)
k = torch.tensor([+0.20, -0.20], dtype=torch.float64)
t = derivative(4, lambda k: torch.func.jacrev(fodo)(x, k), k, jacobian=torch.func.jacfwd)
[6]:
# Set objective function (bx & by at focusing quadrupole center)
from twiss import twiss
from twiss import wolski_to_cs
dk = torch.tensor([0.0, 0.0], dtype=torch.float64)
BX, BY = torch.tensor([25.0, 5.0], dtype=torch.float64)
def objective(k):
m = evaluate(t, [k])
*_, w = twiss(m)
ax, bx, ay, by = wolski_to_cs(w)
return torch.stack([bx, by])
[7]:
# Define model
class Model(torch.nn.Module):
def __init__(self, objective, knobs):
super().__init__()
self.objective = objective
self.knobs = torch.nn.Parameter(torch.clone(knobs))
def forward(self):
return self.objective(self.knobs)
model = Model(objective, dk)
[8]:
# Set optimizer
optimizer = torch.optim.Adam(model.parameters(), lr=0.005)
[9]:
# Set loss function
mse = torch.nn.MSELoss()
[10]:
# Train
model.train()
data = []
for _ in range(256):
beta = model()
loss = mse(beta, torch.stack([BX, BY]))
loss.backward()
optimizer.step()
optimizer.zero_grad()
data.append(loss.item())
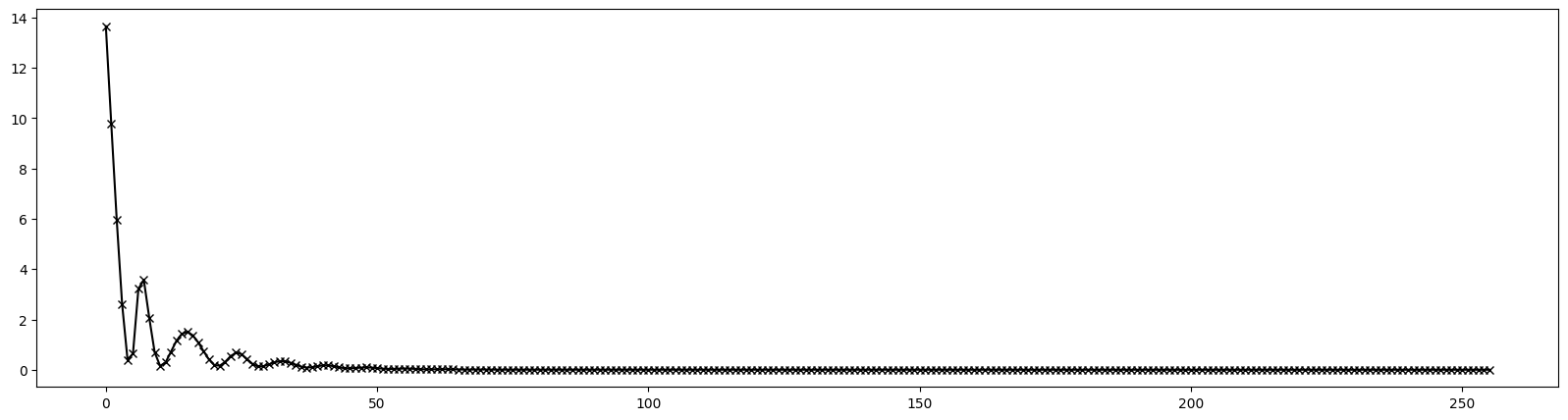
[11]:
# Plot loss
from matplotlib import pyplot as plt
plt.figure(figsize=(20, 5))
plt.plot(range(256), data, color='black', marker='x')
plt.show()
[12]:
# Check result
dk = torch.stack([*model.parameters()]).detach().squeeze()
m = torch.func.jacrev(fodo)(x, k + dk)
*_, w = twiss(m)
ax, bx, ay, by = wolski_to_cs(w)
print(torch.stack([bx, by]))
tensor([2.500e+01, 5.000e+00], dtype=torch.float64)
Example-09: Matched distribution
[1]:
import torch
torch.set_printoptions(precision=3, sci_mode=True)
[2]:
# Set elements
def drif(x, l):
(qx, px, qy, py), l = x, l
return torch.stack([qx + l*px, px, qy + l*py, py])
def quad(x, kn, ks, l, n=25):
(qx, px, qy, py), kn, ks, l = x, kn, ks, l/(2.0*n)
for _ in range(n):
qx, qy = qx + l*px, qy + l*py
px, py = px - 2.0*l*(kn*qx - ks*qy), py + 2.0*l*(ks*qx + kn*qy)
qx, qy = qx + l*px, qy + l*py
return torch.stack([qx, px, qy, py])
[3]:
# Set transport maps
def m11(x, k): kn1, ks1, kn2, ks2 = k; return x
def m12(x, k): kn1, ks1, kn2, ks2 = k; x = drif(x, 5.0); return x
def m23(x, k): kn1, ks1, kn2, ks2 = k; x = quad(x, kn2, ks2, 1.0); return x
def m34(x, k): kn1, ks1, kn2, ks2 = k; x = drif(x, 5.0); return x
def m45(x, k): kn1, ks1, kn2, ks2 = k; x = quad(x, kn1, ks1, 1.0); return x
[4]:
# Set fodo cell
def fodo(x, k):
x = m11(x, k)
x = m12(x, k)
x = m23(x, k)
x = m34(x, k)
x = m45(x, k)
return x
[5]:
# Compute one-turn transport matrix
x = torch.tensor([0.0, 0.0, 0.0, 0.0], dtype=torch.float64)
k = torch.tensor([0.20, -0.01, -0.25, 0.01], dtype=torch.float64)
m = torch.func.jacrev(fodo)(x, k)
print(m)
from twiss.wolski import is_stable
print(is_stable(m))
tensor([[ 2.443e+00, 1.933e+01, 6.129e-02, 3.072e-01],
[-2.357e-01, -1.454e+00, 2.789e-03, -4.458e-02],
[ 5.838e-02, 2.911e-01, -6.017e-01, 3.789e+00],
[-3.216e-03, -7.752e-02, -3.310e-01, 4.167e-01]], dtype=torch.float64)
True
[6]:
# Compute coupled twiss parameters
from twiss import twiss
*_, ws = twiss(m)
[7]:
# Generate beam
from torch.distributions.multivariate_normal import MultivariateNormal
ex = 1.0E-6
ey = 1.0E-8
wx, wy = ws
mean = torch.zeros(4, dtype=torch.float64)
covariance_matrix = ex*wx + ey*wy
distribution = MultivariateNormal(mean, covariance_matrix)
beam = distribution.sample((2**14, )).T
print(covariance_matrix)
print()
print(distribution.covariance_matrix)
print()
print(beam.cov())
print()
tensor([[ 2.224e-05, -2.241e-06, 2.924e-07, -8.274e-08],
[-2.241e-06, 2.709e-07, -3.030e-08, 7.656e-09],
[ 2.924e-07, -3.030e-08, 4.186e-08, 4.045e-09],
[-8.274e-08, 7.656e-09, 4.045e-09, 3.639e-09]], dtype=torch.float64)
tensor([[ 2.224e-05, -2.241e-06, 2.924e-07, -8.274e-08],
[-2.241e-06, 2.709e-07, -3.030e-08, 7.656e-09],
[ 2.924e-07, -3.030e-08, 4.186e-08, 4.045e-09],
[-8.274e-08, 7.656e-09, 4.045e-09, 3.639e-09]], dtype=torch.float64)
tensor([[ 2.223e-05, -2.246e-06, 2.874e-07, -8.269e-08],
[-2.246e-06, 2.726e-07, -3.022e-08, 7.830e-09],
[ 2.874e-07, -3.022e-08, 4.217e-08, 4.078e-09],
[-8.269e-08, 7.830e-09, 4.078e-09, 3.673e-09]], dtype=torch.float64)
[8]:
# Same with distribution function
from twiss import normal
bd = normal(mean, torch.tensor([ex, ey], dtype=torch.float64), ws)
beam = bd.sample((2**16, )).T
print(bd.covariance_matrix)
print()
print(beam.cov())
print()
tensor([[ 2.224e-05, -2.241e-06, 2.924e-07, -8.274e-08],
[-2.241e-06, 2.709e-07, -3.030e-08, 7.656e-09],
[ 2.924e-07, -3.030e-08, 4.186e-08, 4.045e-09],
[-8.274e-08, 7.656e-09, 4.045e-09, 3.639e-09]], dtype=torch.float64)
tensor([[ 2.215e-05, -2.234e-06, 2.895e-07, -8.329e-08],
[-2.234e-06, 2.699e-07, -2.991e-08, 7.692e-09],
[ 2.895e-07, -2.991e-08, 4.185e-08, 4.045e-09],
[-8.329e-08, 7.692e-09, 4.045e-09, 3.650e-09]], dtype=torch.float64)
[9]:
# Transformed beam covariance matrix (matrix)
print((m @ beam).cov())
tensor([[ 2.209e-05, -2.227e-06, 2.863e-07, -8.293e-08],
[-2.227e-06, 2.694e-07, -2.968e-08, 7.647e-09],
[ 2.863e-07, -2.968e-08, 4.182e-08, 4.077e-09],
[-8.293e-08, 7.647e-09, 4.077e-09, 3.650e-09]], dtype=torch.float64)
[10]:
# Transformed beam covariance matrix (map)
beam = torch.func.vmap(lambda x: fodo(x, k))(beam.T).T
print(beam.cov())
tensor([[ 2.209e-05, -2.227e-06, 2.863e-07, -8.293e-08],
[-2.227e-06, 2.694e-07, -2.968e-08, 7.647e-09],
[ 2.863e-07, -2.968e-08, 4.182e-08, 4.077e-09],
[-8.293e-08, 7.647e-09, 4.077e-09, 3.650e-09]], dtype=torch.float64)
[11]:
# Prepare data frame for plotting
import pandas
df = pandas.DataFrame(beam.T.cpu().numpy())
df.columns = ['qx', 'px', 'qy', 'py']
df
[11]:
| qx | px | qy | py | |
|---|---|---|---|---|
| 0 | -0.005472 | 0.000417 | 0.000104 | 0.000064 |
| 1 | -0.002620 | 0.000006 | 0.000144 | 0.000058 |
| 2 | -0.006187 | 0.000686 | -0.000392 | -0.000012 |
| 3 | 0.004921 | -0.000598 | 0.000285 | -0.000008 |
| 4 | 0.000305 | -0.000059 | -0.000060 | -0.000067 |
| ... | ... | ... | ... | ... |
| 65531 | 0.004505 | -0.000694 | 0.000119 | 0.000035 |
| 65532 | -0.006830 | 0.000694 | -0.000085 | 0.000006 |
| 65533 | -0.006022 | 0.000519 | -0.000034 | -0.000057 |
| 65534 | -0.004400 | 0.000133 | -0.000101 | -0.000076 |
| 65535 | 0.001186 | -0.000023 | 0.000396 | 0.000022 |
65536 rows × 4 columns
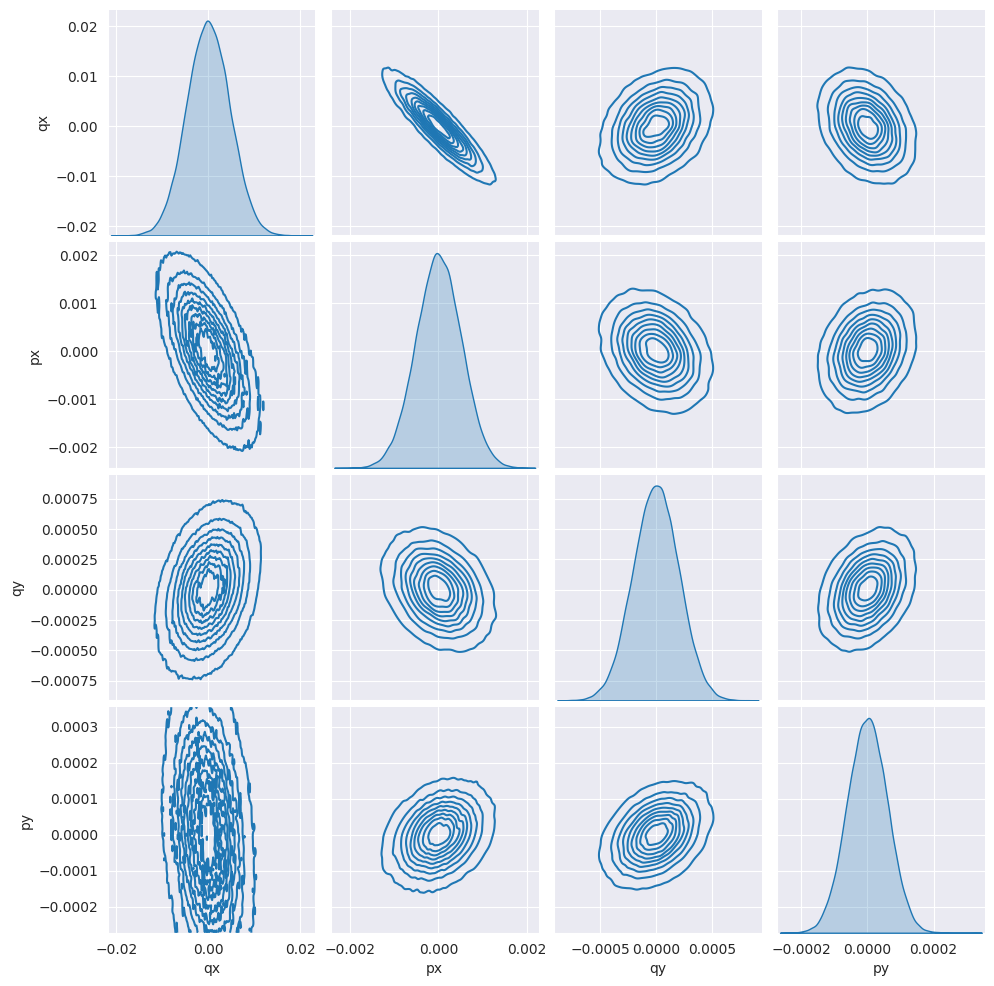
[12]:
# Plot beam
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('darkgrid')
sns.pairplot(df, kind='kde')
plt.show()
[ ]: