Example-17: Line (element)
[1]:
# In this example line usage is illustrated
[2]:
from pathlib import Path
from os import system
from pprint import pprint
import matplotlib
from matplotlib import pyplot as plt
matplotlib.rcParams['text.usetex'] = True
import torch
from model.library.drift import Drift
from model.library.quadrupole import Quadrupole
from model.library.sextupole import Sextupole
from model.library.dipole import Dipole
from model.library.line import Line
[3]:
# Define unique elements
QF = Quadrupole('QF', 0.5, +0.25)
QD = Quadrupole('QD', 0.5, -0.20)
SF = Sextupole('SF', 0.25)
SD = Sextupole('SD', 0.25)
DR = Drift('DR', 0.25)
BM = Dipole('BM', 3.50, torch.pi/8.0)
[4]:
# Define a line
# With propagate flag, values for other flags will be propagated to all root elements (but not to lines!)
FODO = Line('FODO',
[QF, DR, SF, DR, BM, DR, SD, DR, QD, QD, DR, SD, DR, BM, DR, SF, DR, QF],
propagate=True,
dp=0.0,
exact=False,
output=False,
matrix = False)
[5]:
# Similar to elements, lines have to variants of call method
# 1) without deviation variables
state = torch.tensor([0.0, 0.0, 0.0, 0.0], dtype=torch.float64)
print(FODO(state))
# 2) without deviation variables (defaut dictionary)
state = torch.tensor([0.0, 0.0, 0.0, 0.0], dtype=torch.float64)
print(FODO(state, data=FODO.data()))
# In both cases, it is possible to apply alignments errors using alignment flag
# Alignment errors can be applied to elements
tensor([0., 0., 0., 0.], dtype=torch.float64)
tensor([0., 0., 0., 0.], dtype=torch.float64)
[6]:
# Values of deviation variables can be passed only to unique elements
pprint(FODO.data(alignment=False))
{'BM': {'dl': tensor(0., dtype=torch.float64),
'dp': tensor(0., dtype=torch.float64),
'dw': tensor(0., dtype=torch.float64),
'e1': tensor(0., dtype=torch.float64),
'e2': tensor(0., dtype=torch.float64),
'kn': tensor(0., dtype=torch.float64),
'ks': tensor(0., dtype=torch.float64),
'mo': tensor(0., dtype=torch.float64),
'ms': tensor(0., dtype=torch.float64)},
'DR': {'dl': tensor(0., dtype=torch.float64),
'dp': tensor(0., dtype=torch.float64)},
'QD': {'dl': tensor(0., dtype=torch.float64),
'dp': tensor(0., dtype=torch.float64),
'kn': tensor(0., dtype=torch.float64),
'ks': tensor(0., dtype=torch.float64)},
'QF': {'dl': tensor(0., dtype=torch.float64),
'dp': tensor(0., dtype=torch.float64),
'kn': tensor(0., dtype=torch.float64),
'ks': tensor(0., dtype=torch.float64)},
'SD': {'dl': tensor(0., dtype=torch.float64),
'dp': tensor(0., dtype=torch.float64),
'ms': tensor(0., dtype=torch.float64)},
'SF': {'dl': tensor(0., dtype=torch.float64),
'dp': tensor(0., dtype=torch.float64),
'ms': tensor(0., dtype=torch.float64)}}
[7]:
# Mapping over a set of initial conditions
state = 1.0E-3*torch.randn((512, 4), dtype=FODO.dtype, device=FODO.device)
print(torch.vmap(FODO)(state).shape)
torch.Size([512, 4])
[8]:
# Mapping over a set of initial conditions and parameters
state = 1.0E-3*torch.randn((512, 4), dtype=FODO.dtype, device=FODO.device)
dknqf = 1.0E-3*torch.randn(512, dtype=FODO.dtype, device=FODO.device)
def wrapper(state, dknqf):
data = FODO.data()
data['QF']['kn'] = dknqf
return FODO(state, data=data)
print(torch.vmap(wrapper)(state, dknqf).shape)
torch.Size([512, 4])
[9]:
# Differentiability (state)
state = torch.tensor([0.0, 0.0, 0.0, 0.0], dtype=torch.float64)
print(torch.func.jacrev(FODO)(state))
tensor([[-0.4395, 15.4433, 0.0000, 0.0000],
[-0.0522, -0.4395, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.4963, 5.3596],
[ 0.0000, 0.0000, -0.1406, 0.4963]], dtype=torch.float64)
[10]:
# Differentiability (parameter)
state = torch.tensor([0.0, 0.0, 0.0, 0.0], dtype=torch.float64)
dknqf = torch.tensor(0.0, dtype=torch.float64)
def wrapper(dknqf):
data = FODO.data()
data['QF']['kn'] = dknqf
return FODO(state, data=data)
print(torch.func.jacrev(wrapper)(dknqf))
tensor([0., 0., 0., 0.], dtype=torch.float64)
[11]:
# Differentiability (composed)
state = torch.tensor([0.0, 0.0, 0.0, 0.0], dtype=torch.float64)
dknqf = torch.tensor(0.0, dtype=torch.float64)
def wrapper(dknqf):
data = FODO.data()
data['QF']['kn'] = dknqf
return torch.func.jacrev(lambda state, data: FODO(state, data=data))(state, data)
print(wrapper(dknqf))
print(torch.func.jacrev(wrapper)(dknqf))
tensor([[-0.4395, 15.4433, 0.0000, 0.0000],
[-0.0522, -0.4395, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.4963, 5.3596],
[ 0.0000, 0.0000, -0.1406, 0.4963]], dtype=torch.float64)
tensor([[-7.5649, -3.8172, 0.0000, 0.0000],
[ 0.4176, -7.5649, 0.0000, 0.0000],
[ 0.0000, 0.0000, 2.7423, 1.3262],
[ 0.0000, 0.0000, 0.5426, 2.7423]], dtype=torch.float64)
[12]:
%%time
# Tracking
# Note, in general tracking is slow
# This is especially the case for exact integration of elements with large number of slices
qx = torch.linspace(0.0, 0.01, 16, dtype=torch.float64)
px = torch.zeros_like(qx)
qy = torch.zeros_like(qx)
py = torch.zeros_like(qx)
state = torch.stack([qx, px, qy, py]).T
orbit = []
for _ in range(2**10):
state = torch.vmap(FODO)(state)
orbit.append(state)
qx, px, *_ = torch.stack(orbit).swapaxes(0, -1)
CPU times: user 8.17 s, sys: 2.67 ms, total: 8.18 s
Wall time: 8.18 s
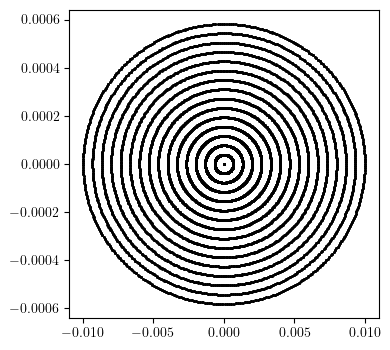
[13]:
# Plot trajectories
plt.figure(figsize=(4, 4))
plt.scatter(qx.cpu().numpy(), px.cpu().numpy(), s=1, color='black')
plt.show()
[14]:
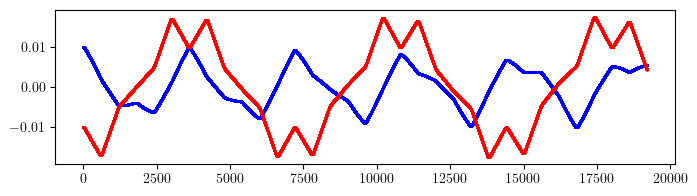
%%time
# Output can be collected at each integration step
# Note, container is overwritten at each call
FODO.ns = 0.01
FODO.output = True
state = torch.tensor([+0.01, 0.0, -0.01, 0.0], dtype=torch.float64)
orbit = []
for _ in range(16):
state = FODO(state)
orbit.append(FODO.container_output)
qx, _, qy, _ = torch.vstack(orbit).T
plt.figure(figsize=(8, 2))
plt.scatter(range(len(qx)), qx.cpu().numpy(), s=1, color='blue')
plt.scatter(range(len(qy)), qy.cpu().numpy(), s=1, color='red')
plt.show()
CPU times: user 14 s, sys: 159 ms, total: 14.2 s
Wall time: 14 s
[15]:
%%time
# Functions can be compiled, but note that dynamo unrolls loops completely (torch 2.4)
# This leads to very long compilation times
FODO.ns = 1
state = torch.tensor([0.0, 0.0, 0.0, 0.0], dtype=torch.float64)
table = 1.0E-3*torch.randn((512, 4), dtype=FODO.dtype, device=FODO.device)
fodo = torch.compile(FODO)
fodo(state)
CPU times: user 17.8 s, sys: 5.1 s, total: 22.9 s
Wall time: 24.8 s
[15]:
tensor([0., 0., 0., 0.], dtype=torch.float64)
[16]:
%%timeit
FODO(state)
4.71 ms ± 57.9 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
[17]:
%%timeit
fodo(state)
458 µs ± 2.08 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
[18]:
%%timeit
_ = torch.vmap(FODO)(table)
8.5 ms ± 46.9 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
[19]:
%%timeit
_ = torch.vmap(fodo)(table)
8.89 ms ± 514 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
[20]:
# Note, compositional operations (map or jacobian seems to break/ignore compiled version)
[21]:
# name (property)
# This property can be used to get/set line name
FODO.name
[21]:
'FODO'
[22]:
# sequence (property)
# Contains ordered sequence of elements
# Elements can be added or removed from it
len(FODO.sequence)
[22]:
18
[23]:
# unique (property)
# name: (type, length, angle) data for all unique elements
pprint(FODO.unique)
{'BM': ('Dipole',
tensor(3.5000, dtype=torch.float64),
tensor(0.3927, dtype=torch.float64)),
'DR': ('Drift',
tensor(0.2500, dtype=torch.float64),
tensor(0., dtype=torch.float64)),
'QD': ('Quadrupole',
tensor(0.5000, dtype=torch.float64),
tensor(0., dtype=torch.float64)),
'QF': ('Quadrupole',
tensor(0.5000, dtype=torch.float64),
tensor(0., dtype=torch.float64)),
'SD': ('Sextupole',
tensor(0.2500, dtype=torch.float64),
tensor(0., dtype=torch.float64)),
'SF': ('Sextupole',
tensor(0.2500, dtype=torch.float64),
tensor(0., dtype=torch.float64))}
[24]:
# length (property)
FODO.length
[24]:
tensor(12., dtype=torch.float64)
[25]:
# angle (property)
FODO.angle
[25]:
tensor(0.7854, dtype=torch.float64)
[26]:
# ns (property)
# This property can be used to get/set number of integration steps to unique elements
# Set value integration steps to all elements
FODO.ns = 10
print(FODO.ns)
# Set ceil(element.length/value) integration steps to each element
FODO.ns = 0.1
print(FODO.ns)
# Set by name or type
FODO.ns = (('DR', 1), ('Sextupole', 0.01))
print(FODO.ns)
{'QF': 10, 'DR': 10, 'SF': 10, 'BM': 10, 'SD': 10, 'QD': 10}
{'QF': 5, 'DR': 3, 'SF': 3, 'BM': 35, 'SD': 3, 'QD': 5}
{'QF': 5, 'DR': 1, 'SF': 25, 'BM': 35, 'SD': 25, 'QD': 5}
[27]:
# order (property)
# This property can be used to get/set integration order to unique elements
# Set value integration steps to all elements
FODO.order = 0
print(FODO.order)
# Set by name or type
FODO.order = (('BM', 1), ('Sextupole', 1))
print(FODO.order)
{'QF': 0, 'DR': 0, 'SF': 0, 'BM': 0, 'SD': 0, 'QD': 0}
{'QF': 0, 'DR': 0, 'SF': 1, 'BM': 1, 'SD': 1, 'QD': 0}
[28]:
# Nested lines
FODO = Line('FODO', [QF, DR, SF, DR, BM, DR, SD, DR, QD, QD, DR, SD, DR, BM, DR, SF, DR, QF], propagate=True, dp=0.0, exact=False, output=False, matrix = False)
RING = Line('RING', 8*[FODO], propagate=True, dp=0.0, exact=False, output=False, matrix = False)
RING.ns = 1
print(RING.ns)
RING.order = 0
print(RING.order)
# Note, sublines are not flattened
print(len(RING.sequence))
{'QF': 1, 'DR': 1, 'SF': 1, 'BM': 1, 'SD': 1, 'QD': 1}
{'QF': 0, 'DR': 0, 'SF': 0, 'BM': 0, 'SD': 0, 'QD': 0}
8
[29]:
# Tracking, mapping and differentiation is similar to flat lines
state = torch.tensor([0.0, 0.0, 0.0, 0.0], dtype=torch.float64)
RING(state)
[29]:
tensor([0., 0., 0., 0.], dtype=torch.float64)
[30]:
# Deviation table contains unique lines with unique elements (unique by names)
pprint(RING.data(alignment=False))
{'FODO': {'BM': {'dl': tensor(0., dtype=torch.float64),
'dp': tensor(0., dtype=torch.float64),
'dw': tensor(0., dtype=torch.float64),
'e1': tensor(0., dtype=torch.float64),
'e2': tensor(0., dtype=torch.float64),
'kn': tensor(0., dtype=torch.float64),
'ks': tensor(0., dtype=torch.float64),
'mo': tensor(0., dtype=torch.float64),
'ms': tensor(0., dtype=torch.float64)},
'DR': {'dl': tensor(0., dtype=torch.float64),
'dp': tensor(0., dtype=torch.float64)},
'QD': {'dl': tensor(0., dtype=torch.float64),
'dp': tensor(0., dtype=torch.float64),
'kn': tensor(0., dtype=torch.float64),
'ks': tensor(0., dtype=torch.float64)},
'QF': {'dl': tensor(0., dtype=torch.float64),
'dp': tensor(0., dtype=torch.float64),
'kn': tensor(0., dtype=torch.float64),
'ks': tensor(0., dtype=torch.float64)},
'SD': {'dl': tensor(0., dtype=torch.float64),
'dp': tensor(0., dtype=torch.float64),
'ms': tensor(0., dtype=torch.float64)},
'SF': {'dl': tensor(0., dtype=torch.float64),
'dp': tensor(0., dtype=torch.float64),
'ms': tensor(0., dtype=torch.float64)}}}
[31]:
# If this can be used to pass different values of deviation variables to unique elements
# But values should match for consistent differentiation
LA = Line('LA', [QF, DR, SF, DR, BM, DR, SD, DR, QD, QD, DR, SD, DR, BM, DR, SF, DR, QF], propagate=True, dp=0.0, exact=False, output=False, matrix = False)
LB = Line('LB', [QF, DR, SF, DR, BM, DR, SD, DR, QD, QD, DR, SD, DR, BM, DR, SF, DR, QF], propagate=True, dp=0.0, exact=False, output=False, matrix = False)
RING = Line('RING', [LA, LB], propagate=True, dp=0.0, exact=False, output=False, matrix = False)
state = torch.tensor([0.01, 0.0, 0.01, 0.0], dtype=torch.float64)
kn = torch.tensor(0.01, dtype=torch.float64)
data = RING.data()
data['LA']['QF']['kn'] = kn
data['LB']['QF']['kn'] = kn
print(RING(state, data=data))
kna = torch.tensor(+0.01, dtype=torch.float64)
knb = torch.tensor(-0.01, dtype=torch.float64)
data['LA']['QF']['kn'] = kna
data['LB']['QF']['kn'] = knb
print(RING(state, data=data))
tensor([-0.0047, 0.0005, -0.0045, -0.0014], dtype=torch.float64)
tensor([-0.0055, 0.0005, -0.0048, -0.0014], dtype=torch.float64)
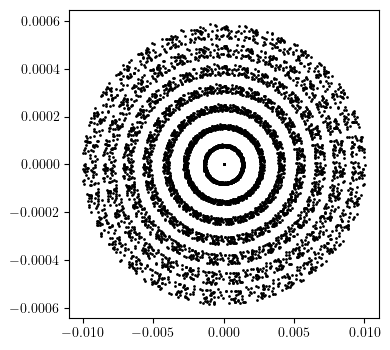
[32]:
# Modulation
FODO = Line('FODO', [QF, DR, SF, DR, BM, DR, SD, DR, QD, QD, DR, SD, DR, BM, DR, SF, DR, QF], propagate=True, dp=0.0, exact=False, output=False, matrix = False)
dkf = 1.0E-3*torch.randn(2**10, dtype=torch.float64)
dkd = 1.0E-3*torch.randn(2**10, dtype=torch.float64)
qx = torch.linspace(0.0, 0.01, 8, dtype=torch.float64)
px = torch.zeros_like(qx)
qy = torch.zeros_like(qx)
py = torch.zeros_like(qx)
state = torch.stack([qx, px, qy, py]).T
orbit = []
data = FODO.data()
for i in range(2**10):
data['QF']['kn'] = dkf[i]
data['QD']['kn'] = dkd[i]
state = torch.vmap(lambda state: FODO(state, data=data))(state)
orbit.append(state)
qx, px, *_ = torch.stack(orbit).swapaxes(0, -1)
plt.figure(figsize=(4, 4))
plt.scatter(qx.cpu().numpy(), px.cpu().numpy(), s=1, color='black')
plt.show()
[33]:
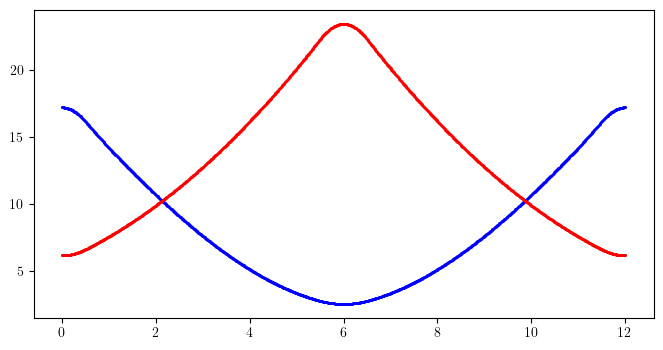
# Matrix output and twiss parameters
from twiss import twiss
from twiss import propagate
from twiss import wolski_to_cs
QF = Quadrupole('QF', 0.5, +0.25)
QD = Quadrupole('QD', 0.5, -0.20)
SF = Sextupole('SF', 0.25)
SD = Sextupole('SD', 0.25)
DR = Drift('DR', 0.25)
BM = Dipole('BM', 3.50, torch.pi/8.0)
FODO = Line('FODO', [QF, DR, SF, DR, BM, DR, SD, DR, QD, QD, DR, SD, DR, BM, DR, SF, DR, QF], propagate=True, matrix=True)
FODO.ns = 0.01
state = torch.tensor([0.0, 0.0, 0.0, 0.0], dtype=torch.float64)
print(torch.func.jacrev(FODO)(state))
print()
out, *ms = FODO.container_matrix
for m in ms:
out = m @ out
print(out)
print()
*_, w = twiss(out)
ws = [w]
for m in FODO.container_matrix:
w = propagate(w, m)
ws.append(w)
ws = torch.stack(ws)
_, bx, _, by = torch.vmap(wolski_to_cs)(ws).T
s = torch.linspace(0.0, 12.0, len(bx), dtype=torch.float64)
plt.figure(figsize=(8, 4))
plt.scatter(s.cpu().numpy(), bx.cpu().numpy(), s=1, color='blue')
plt.scatter(s.cpu().numpy(), by.cpu().numpy(), s=1, color='red')
plt.show()
tensor([[-0.4395, 15.4433, 0.0000, 0.0000],
[-0.0522, -0.4395, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.4963, 5.3596],
[ 0.0000, 0.0000, -0.1406, 0.4963]], dtype=torch.float64)
tensor([[-0.4395, 15.4433, 0.0000, 0.0000],
[-0.0522, -0.4395, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.4963, 5.3596],
[ 0.0000, 0.0000, -0.1406, 0.4963]], dtype=torch.float64)
[34]:
# More line properties
# Define simple FODO based lattice using nested lines
DR = Drift('DR', 0.25)
BM = Dipole('BM', 3.50, torch.pi/4.0)
QF_A = Quadrupole('QF_A', 0.5, +0.20)
QD_A = Quadrupole('QD_A', 0.5, -0.19)
QF_B = Quadrupole('QF_B', 0.5, +0.20)
QD_B = Quadrupole('QD_B', 0.5, -0.19)
QF_C = Quadrupole('QF_C', 0.5, +0.20)
QD_C = Quadrupole('QD_C', 0.5, -0.19)
QF_D = Quadrupole('QF_D', 0.5, +0.20)
QD_D = Quadrupole('QD_D', 0.5, -0.19)
SF_A = Sextupole('SF_A', 0.25, 0.00)
SD_A = Sextupole('SD_A', 0.25, 0.00)
SF_B = Sextupole('SF_B', 0.25, 0.00)
SD_B = Sextupole('SD_B', 0.25, 0.00)
SF_C = Sextupole('SF_C', 0.25, 0.00)
SD_C = Sextupole('SD_C', 0.25, 0.00)
SF_D = Sextupole('SF_D', 0.25, 0.00)
SD_D = Sextupole('SD_D', 0.25, 0.00)
FODO_A = Line('FODO_A', [QF_A, DR, SF_A, DR, BM, DR, SD_A, DR, QD_A, QD_A, DR, SD_A, DR, BM, DR, SF_A, DR, QF_A], propagate=True, dp=0.0, exact=False, output=False, matrix=False)
FODO_B = Line('FODO_B', [QF_B, DR, SF_B, DR, BM, DR, SD_B, DR, QD_B, QD_B, DR, SD_B, DR, BM, DR, SF_B, DR, QF_B], propagate=True, dp=0.0, exact=False, output=False, matrix=False)
FODO_C = Line('FODO_C', [QF_C, DR, SF_C, DR, BM, DR, SD_C, DR, QD_C, QD_C, DR, SD_C, DR, BM, DR, SF_C, DR, QF_C], propagate=True, dp=0.0, exact=False, output=False, matrix=False)
FODO_D = Line('FODO_D', [QF_D, DR, SF_D, DR, BM, DR, SD_D, DR, QD_D, QD_D, DR, SD_D, DR, BM, DR, SF_D, DR, QF_D], propagate=True, dp=0.0, exact=False, output=False, matrix=False)
RING = Line('RING', [FODO_A, FODO_B, FODO_C, FODO_D], propagate=True, dp=0.0, exact=False, output=False, matrix=False)
[35]:
# Name and names
print(FODO_A.name)
print(FODO_A.names)
print()
print(RING.name)
print(RING.names)
print()
FODO_A
['QF_A', 'DR', 'SF_A', 'DR', 'BM', 'DR', 'SD_A', 'DR', 'QD_A', 'QD_A', 'DR', 'SD_A', 'DR', 'BM', 'DR', 'SF_A', 'DR', 'QF_A']
RING
['FODO_A', 'FODO_B', 'FODO_C', 'FODO_D']
[36]:
# Scan (recurcivly traverse lattice and yeild elements with matching attribute)
# All elements, since all elements have a name
print(len([*FODO_A.scan('name')]))
print(len([*RING.scan('name')]))
# All dipoles
print(len([*FODO_A.scan('angle')]))
print(len([*RING.scan('angle')]))
18
72
2
8
[37]:
# Flatten
print(len(RING))
RING.flatten()
print(len(RING))
4
72
[38]:
# First positon of an element
print(FODO_A.position('BM'))
print(FODO_A.names)
4
['QF_A', 'DR', 'SF_A', 'DR', 'BM', 'DR', 'SD_A', 'DR', 'QD_A', 'QD_A', 'DR', 'SD_A', 'DR', 'BM', 'DR', 'SF_A', 'DR', 'QF_A']
[39]:
# Get first element
print(FODO_A.start)
print(FODO_A.names)
QF_A
['QF_A', 'DR', 'SF_A', 'DR', 'BM', 'DR', 'SD_A', 'DR', 'QD_A', 'QD_A', 'DR', 'SD_A', 'DR', 'BM', 'DR', 'SF_A', 'DR', 'QF_A']
[40]:
# Set first element (rotate sequence)
# Note, first mathced occuranve is used
FODO_A.start = 'BM'
print(FODO_A.names)
['BM', 'DR', 'SD_A', 'DR', 'QD_A', 'QD_A', 'DR', 'SD_A', 'DR', 'BM', 'DR', 'SF_A', 'DR', 'QF_A', 'QF_A', 'DR', 'SF_A', 'DR']
[41]:
# Itemize (list of all elements with matching kind)
print(RING.itemize('Sextupole'))
['SF_A', 'SD_A', 'SF_B', 'SD_B', 'SF_C', 'SD_C', 'SF_D', 'SD_D']
[42]:
# Number of first level elements/lines
print(len(RING))
72
[43]:
# Get by index or name (first matched)
print(FODO_B[1])
print(FODO_B['DR'])
Drift(name="DR", length=0.25, dp=0.0, exact=False, ns=1, order=0)
Drift(name="DR", length=0.25, dp=0.0, exact=False, ns=1, order=0)
[44]:
# Set by index or name (first matched)
print(FODO_B.names)
FODO_B['SF_B'] = FODO_B['DR']
print(FODO_B.names)
FODO_B['SF_B'] = FODO_B['DR']
print(FODO_B.names)
['QF_B', 'DR', 'SF_B', 'DR', 'BM', 'DR', 'SD_B', 'DR', 'QD_B', 'QD_B', 'DR', 'SD_B', 'DR', 'BM', 'DR', 'SF_B', 'DR', 'QF_B']
['QF_B', 'DR', 'DR', 'DR', 'BM', 'DR', 'SD_B', 'DR', 'QD_B', 'QD_B', 'DR', 'SD_B', 'DR', 'BM', 'DR', 'SF_B', 'DR', 'QF_B']
['QF_B', 'DR', 'DR', 'DR', 'BM', 'DR', 'SD_B', 'DR', 'QD_B', 'QD_B', 'DR', 'SD_B', 'DR', 'BM', 'DR', 'DR', 'DR', 'QF_B']