Example-57: Trajectory (Approximate invariants spread)

# In this example derivatives of approximate invariants spread with respect to parameters are computed
# Given a set of initial conditions, an objective function can be constructed

# Import

import torch

from matplotlib import pyplot as plt

from model.library.custom import Custom
from model.library.line import Line

from model.command.mapping import mapping
from model.command.trajectory import trajectory

# Define 4D symplectic transformation

nux, nuy = torch.tensor([0.168, 0.201], dtype=torch.float64)
mux, muy = 2*torch.pi*nux, 2*torch.pi*nuy
cx, sx, cy, sy = mux.cos(), mux.sin(), muy.cos(), muy.sin()

def transformation(x, k, dp=None):
    qx, px, qy, py, *_ = x
    return torch.stack([
        cx*qx + sx*(px + qx**2 - qy**2 + k*(qx**3 - 3*qx*qy**2)),
        cx*(px + qx**2 - qy**2 + k*(qx**3 - 3*qx*qy**2)) - sx*qx,
        cy*qy + sy*(py - 2*qx*qy + k*(-3*qx**2*qy + qy**3)),
        cy*(py - 2*qx*qy + k*(-3*qx**2*qy + qy**3)) - sy*qy
    ])

k = torch.tensor(0.0, dtype=torch.float64)
x = torch.tensor([0.0, 0.0, 0.0, 0.0], dtype=torch.float64)

print(x)
print(transformation(x, k))

tensor([0., 0., 0., 0.], dtype=torch.float64)
tensor([0., 0., 0., 0.], dtype=torch.float64)

# Define custom element using the above transformation

custom = Custom('custom', transformation, ['k'])
print(custom(x))

tensor([0., 0., 0., 0.], dtype=torch.float64)

# Define line with a single custom element

ring = Line('ring', [custom])
print(ring(x))

tensor([0., 0., 0., 0.], dtype=torch.float64)

# Test tracking

k = torch.tensor(0, dtype=torch.float64)
x = torch.tensor([0.001, -0.0001, -0.005, 0.0001], dtype=torch.float64)

data = custom.data()
data['k'] = k
print(transformation(x, k) - custom(x, data=data))

data = ring.data()
data['custom']['k'] = k
print(transformation(x, k) - ring(x, data=data))

tensor([0., 0., 0., 0.], dtype=torch.float64)
tensor([0., 0., 0., 0.], dtype=torch.float64)

# Test wrapper

fn, *_ = mapping(ring, 0, 0, ('k', ['Custom'], None, None))

print(transformation(x, k) - fn(x, k.unsqueeze(-1)))

tensor([0., 0., 0., 0.], dtype=torch.float64)

# Test derivatives

k = torch.tensor([0.0], dtype=torch.float64)
x = torch.tensor([0.0, 0.0, 0.0, 0.0], dtype=torch.float64)

print(torch.func.jacrev(transformation)(x, k.squeeze()))
print()

print(torch.func.jacrev(fn)(x, k))
print()

tensor([[ 0.4927,  0.8702,  0.0000,  0.0000],
        [-0.8702,  0.4927,  0.0000,  0.0000],
        [ 0.0000,  0.0000,  0.3030,  0.9530],
        [ 0.0000,  0.0000, -0.9530,  0.3030]], dtype=torch.float64)

tensor([[ 0.4927,  0.8702,  0.0000,  0.0000],
        [-0.8702,  0.4927,  0.0000,  0.0000],
        [ 0.0000,  0.0000,  0.3030,  0.9530],
        [ 0.0000,  0.0000, -0.9530,  0.3030]], dtype=torch.float64)

# Define and test trajectory generator

fn = trajectory(ring, [0], ('k', ['Custom'], None, None))

k = torch.tensor([0.0], dtype=torch.float64)
x = torch.tensor([0.0, 0.0, 0.0, 0.0], dtype=torch.float64)

print(fn(1, x, k))
print()

tensor([[0., 0., 0., 0.],
        [0., 0., 0., 0.]], dtype=torch.float64)

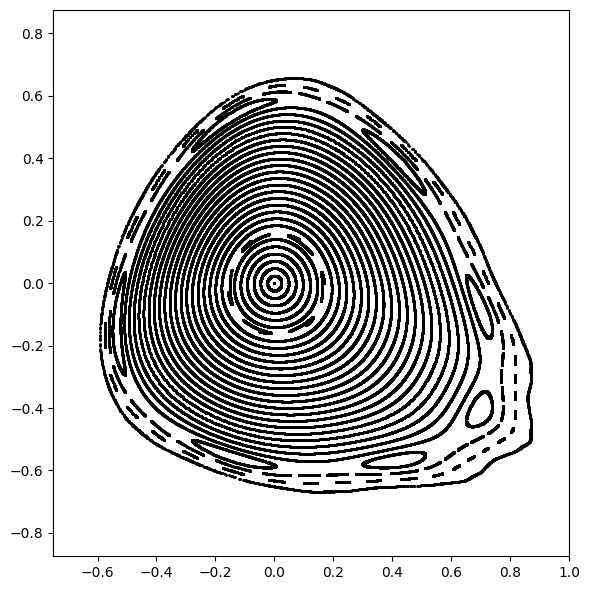
# Generate and plot phase space trajectories in horizontal plane

n = 2**12

k = torch.tensor([0.0], dtype=torch.float64)

qx = torch.linspace(0.00, 0.75, 32, dtype=torch.float64)
px = torch.zeros_like(qx)
qy = torch.zeros_like(qx)
py = torch.zeros_like(qx)

xs = torch.stack([qx, px, qy, py]).T

out = torch.vmap(fn, in_dims=(None, 0, None))(n, xs, k)
qxs, pxs, *_ = out.swapaxes(0, -1)

plt.figure(figsize=(6, 6))
for qx, px in zip(qxs.T, pxs.T):
    plt.errorbar(qx.cpu().numpy(), px.cpu().numpy(), fmt=' ', marker='o', ms=1, color='black')
plt.xlim(-0.750, 1.000)
plt.ylim(-0.875, 0.875)
plt.tight_layout()
plt.show()

# Test linear invariants conservation

# Set approximate invariants

def ix(qx, px, qy, py):
    return 0.5*(qx**2 + px**2)

def iy(qx, px, qy, py):
    return 0.5*(qy**2 + py**2)

# Generate trajectories

n = 2**12

k = torch.tensor([0.0], dtype=torch.float64)

qx = torch.linspace(0.001, 0.250, 16, dtype=torch.float64)
px = torch.zeros_like(qx)
qy = torch.linspace(0.001, 0.250, 16, dtype=torch.float64)
py = torch.zeros_like(qx)

xs = torch.stack([qx, px, qy, py]).T

out = torch.vmap(fn, in_dims=(None, 0, None))(n, xs, k).swapaxes(1, -1)

# Compute invariants

ixs = torch.vmap(lambda trajectory: ix(*trajectory))(out)
iys = torch.vmap(lambda trajectory: iy(*trajectory))(out)

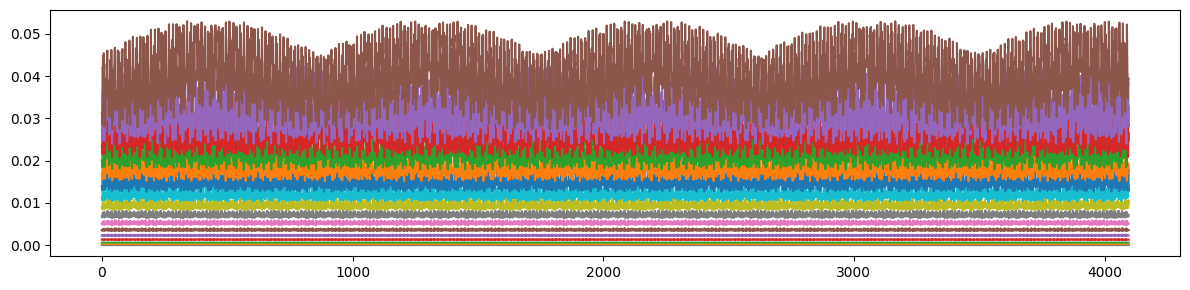
# Plot horizontal invariants vs number of iteration

plt.figure(figsize=(12, 3))
plt.plot(ixs.T.cpu().numpy())
plt.tight_layout()
plt.show()

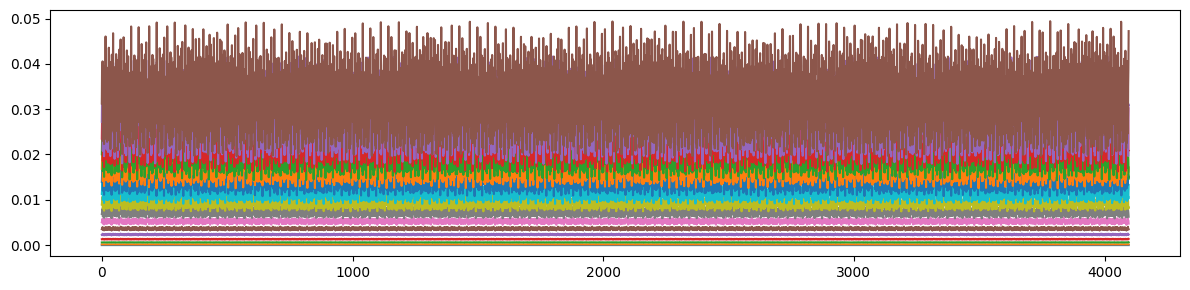
# Plot vertical invariants vs number of iteration

plt.figure(figsize=(12, 3))
plt.plot(iys.T.cpu().numpy())
plt.tight_layout()
plt.show()

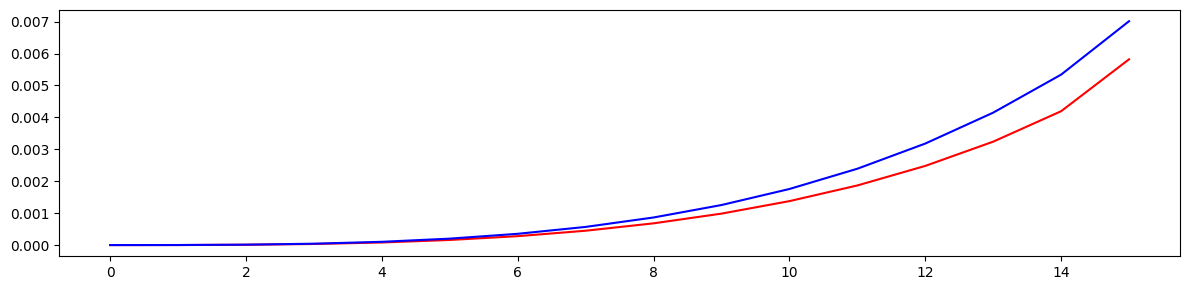
# Plot spead vs amplitude (measure of invariant conservation)

plt.figure(figsize=(12, 3))
plt.plot(ixs.std(-1).cpu().numpy(), color='red')
plt.plot(iys.std(-1).cpu().numpy(), color='blue')
plt.tight_layout()
plt.show()

# Define spread merit function

# Set initial grid

n = 8

qx = torch.linspace(-0.3, 0.3, n, dtype=torch.float64)
qy = torch.linspace(-0.3, 0.3, n, dtype=torch.float64)

qx, qy = torch.stack(torch.meshgrid(qx, qy, indexing='ij')).swapaxes(-1, 0).reshape(n*n, -1).T

px = torch.zeros_like(qx)
py = torch.zeros_like(qy)

xs = torch.stack([qx, px, qy, py]).T

plt.figure(figsize=(4, 4))
plt.errorbar(qx.cpu().numpy(), qy.cpu().numpy(), fmt=' ', marker='o', ms=1, color='black')
plt.tight_layout()
plt.show()

# Define objective (mean spread over initials for each plane)

def objective(k, n=2**10):
    out = torch.vmap(fn, in_dims=(None, 0, None))(n, xs, k).swapaxes(1, -1)
    ixs = torch.vmap(lambda trajectory: ix(*trajectory))(out)
    iys = torch.vmap(lambda trajectory: iy(*trajectory))(out)
    return torch.stack([ixs.std(-1).mean(), iys.std(-1).mean()])

# Test objective

k = torch.tensor([0.0], dtype=torch.float64)

print(objective(k))
print()

tensor([0.0030, 0.0027], dtype=torch.float64)

# Compute derivative

print(torch.func.jacrev(objective)(k))

tensor([[-0.0007],
        [-0.0007]], dtype=torch.float64)