Example-32: Orbit (quadruple shift)
[1]:
# In this example effects of transverse quadrupole shifts on closed orbit are illustrated
# 1st order derivatives of closed orbit are computed
# Surrogate model from derivatives is compared with direct tracking
[2]:
# Import
from pprint import pprint
import torch
from pathlib import Path
import matplotlib
from matplotlib import pyplot as plt
from matplotlib.patches import Rectangle
matplotlib.rcParams['text.usetex'] = True
from twiss import twiss
from model.library.line import Line
from model.command.util import chop
from model.command.util import evaluate
from model.command.util import series
from model.command.external import load_lattice
from model.command.build import build
from model.command.wrapper import group
from model.command.orbit import orbit
from model.command.orbit import parametric_orbit
[3]:
# Build and setup lattice
path = Path('ic.lte')
data = load_lattice(path)
ring:Line = build('RING', 'ELEGANT', data)
ring.propagate = True
ring.flatten()
ring.merge()
ring.split((None, ['BPM'], None, None))
ring.roll(1)
ring.splice()
[4]:
# Compute closed orbit
fp = 1.0E-3*torch.randn(4, dtype=torch.float64)
fp, *_ = orbit(ring, fp, [], alignment=True, limit=8, epsilon=1.0E-12)
# Chop small values
fp = [fp]
chop(fp)
fp, *_ = fp
print(fp)
tensor([0., 0., 0., 0.], dtype=torch.float64)
[5]:
# Compute parametric closed orbit
# Parametric orbit is computed separately for each plane
# Passing both goups together will result in computation of cross derivatives, i.e. d^2(qx, px, qy, py)/d(dx)d(dy)
# Also, since only the first order derivatives are computed, there is no interaction and they can be computed separatly for each element (selected name)
# Note, computation speed is moderate for 1st order derivatives
# Higher order derivatives computation time grows exponentially, so as grows memory requirements with torch.func.jacrev
# In memory limmited case, torch.func.jacfwd can be used, which requires less memory, but also much slower than torch.func.jacrev
n_quad = ring.describe['Quadrupole']
dx = torch.tensor(n_quad*[0.0], dtype=torch.float64)
dy = torch.tensor(n_quad*[0.0], dtype=torch.float64)
pox, *_ = parametric_orbit(ring,
fp,
[dx],
(1, 'dx', ['Quadrupole'], None, None),
alignment=True,
advance=True,
full=False,
jacobian=torch.func.jacrev)
poy, *_ = parametric_orbit(ring,
fp,
[dy],
(1, 'dy', ['Quadrupole'], None, None),
alignment=True,
advance=True,
full=False,
jacobian=torch.func.jacrev)
chop(pox)
chop(poy)
[6]:
# Compute only for selected quadrupole (the first one)
name, *_ = [name for name, kind, *_ in ring.layout() if kind == 'Quadrupole']
# Adjust deviation variables
dx = torch.tensor(1*[0.0], dtype=torch.float64)
dy = torch.tensor(1*[0.0], dtype=torch.float64)
# Compute d(qx,px,qy,py) / d(dx)
data, *_ = parametric_orbit(ring, fp, [dx], (1, 'dx', None, [name], None), alignment=True, advance=False)
chop(data)
pprint(data)
print()
# Compute d(qx,px,qy,py) / d(dy)
data, *_ = parametric_orbit(ring, fp, [dy], (1, 'dy', None, [name], None), alignment=True, advance=False)
chop(data)
pprint(data)
print()
# With two groups the following in computed
# d (qx,px,qy,py) / d(dx)
# d (qx,px,qy,py) / d(dy)
# d^2 (qx,px,qy,py) / d(dx)d(dy)
data, *_ = parametric_orbit(ring, fp, [dx, dy], (1, 'dx', None, [name], None), (1, 'dy', None, [name], None), alignment=True, advance=False)
chop(data)
pprint(data)
print()
[[tensor([0., 0., 0., 0.], dtype=torch.float64),
tensor([[ 1.8121],
[-2.6451],
[ 0.0000],
[ 0.0000]], dtype=torch.float64)]]
[[tensor([0., 0., 0., 0.], dtype=torch.float64),
tensor([[ 0.0000],
[ 0.0000],
[ -5.5153],
[-10.0840]], dtype=torch.float64)]]
[[[tensor([0., 0., 0., 0.], dtype=torch.float64),
tensor([[ 0.0000],
[ 0.0000],
[ -5.5153],
[-10.0840]], dtype=torch.float64)],
[tensor([[ 1.8121],
[-2.6451],
[ 0.0000],
[ 0.0000]], dtype=torch.float64),
tensor([[[ 0.0000]],
[[ 0.0000]],
[[-378.9334]],
[[-585.2541]]], dtype=torch.float64)]]]
[7]:
# Compare with results for all quadrupoles
local, *_ = pox
pprint(local)
print()
local, *_ = poy
pprint(local)
print()
[[tensor([0., 0., 0., 0.], dtype=torch.float64),
tensor([[ 1.8121, -0.7183, 5.5918, -2.6908, -1.4942, 0.3195, -0.8425,
2.7908, 1.4097, -4.9412, 0.5832, -2.2199, 4.1151, 4.3880,
-2.5482, 0.2864, -3.0901, -1.1294, 4.8129, -1.6948, -0.6838,
1.0844, -4.6974, 6.1343, -0.8751, 1.0602, -2.4840, -3.2927],
[ -2.6451, 1.4732, -10.9761, 6.8781, 0.4980, 0.3000, 2.3551,
-7.0806, -0.3743, 7.6515, -0.8327, 4.4808, -8.0043, -8.0279,
4.5093, -0.8070, 7.4910, -0.1542, -7.2558, 2.4290, 0.3869,
0.2745, 7.0520, -11.1285, 1.5267, -2.7711, 5.8554, 6.9226],
[ 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000]],
dtype=torch.float64)]]
[[tensor([0., 0., 0., 0.], dtype=torch.float64),
tensor([[ 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[ -5.5153, -0.8035, 1.3808, -2.2944, -3.9345, 1.9563, 0.4778,
0.3985, 2.8365, 2.7562, -0.4292, 0.4229, -0.7416, -3.5727,
6.3601, 1.1415, -3.0089, 1.2609, 4.4112, -2.5337, -1.5453,
1.5144, -2.1693, -3.9671, 0.9664, 2.2998, -0.8209, 3.0710],
[-10.0840, -1.6969, 3.8276, -2.9874, -7.1554, 3.8655, 1.7814,
-1.0479, 4.2450, 5.7689, -1.1597, -1.7639, 0.1496, -5.6754,
10.4517, 2.0721, -6.0926, 1.0031, 7.2082, -4.4147, -3.3390,
4.0558, -2.7299, -7.1642, 1.9402, 5.9765, -2.6801, 4.2593]],
dtype=torch.float64)]]
[8]:
# Compare orbit response for a single random realization
# Set errors
dx = 50.0E-6*torch.randn(n_quad, dtype=torch.float64)
dy = 50.0E-6*torch.randn(n_quad, dtype=torch.float64)
# Compute closed orbit at all BPMs
# Note, alignment is on
points, *_ = orbit(ring, fp, [dx, dy], ('dx', ['Quadrupole'], None, None), ('dy', ['Quadrupole'], None, None), alignment=True, advance=True, full=False, limit=16, epsilon=1.0E-12)
# Test closed orbit
# Set parametric ring
start, *_, end = ring.names
mapping, *_ = group(ring, start, end, ('dx', ['Quadrupole'], None, None), ('dy', ['Quadrupole'], None, None), alignment=True)
# Propagate estimated closed orbit
point, *_ = points
print(point)
print(mapping(point, dx, dy))
print(torch.allclose(point, mapping(point, dx, dy), rtol=1.0E-12, atol=1.0E-12))
print()
# Evaluate parametric fixed point for given deviations
local, *_ = pox
print(evaluate(local, [fp, dx]))
local, *_ = poy
print(evaluate(local, [fp, dy]))
print()
# Plot orbit at all locations
qx, px, qy, py = points.T
Qx, Px, *_ = torch.stack([evaluate(local, [fp, dx]) for local in pox]).T
*_, Qy, Py = torch.stack([evaluate(local, [fp, dy]) for local in poy]).T
# qx vs Qx
plt.figure(figsize=(16, 2))
plt.errorbar(ring.locations().cpu().numpy(), qx.cpu().numpy(), fmt='-', color='blue', marker='o', ms=8, alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), Qx.cpu().numpy(), fmt=' ', color='black', marker='x', ms=8, alpha=1)
plt.xticks(ticks=ring.locations(), labels=dict.fromkeys([name for name, kind, *_ in ring.layout() if kind == 'BPM']))
plt.tight_layout()
plt.show()
# px vs Px
plt.figure(figsize=(16, 2))
plt.errorbar(ring.locations().cpu().numpy(), px.cpu().numpy(), fmt='-', color='blue', marker='o', ms=8, alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), Px.cpu().numpy(), fmt=' ', color='black', marker='x', ms=8, alpha=1)
plt.xticks(ticks=ring.locations(), labels=dict.fromkeys([name for name, kind, *_ in ring.layout() if kind == 'BPM']))
plt.tight_layout()
plt.show()
# qy vs Qy
plt.figure(figsize=(16, 2))
plt.errorbar(ring.locations().cpu().numpy(), qy.cpu().numpy(), fmt='-', color='blue', marker='o', ms=8, alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), Qy.cpu().numpy(), fmt=' ', color='black', marker='x', ms=8, alpha=1)
plt.xticks(ticks=ring.locations(), labels=dict.fromkeys([name for name, kind, *_ in ring.layout() if kind == 'BPM']))
plt.tight_layout()
plt.show()
# py vs Py
plt.figure(figsize=(16, 2))
plt.errorbar(ring.locations().cpu().numpy(), py.cpu().numpy(), fmt='-', color='blue', marker='o', ms=8, alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), Py.cpu().numpy(), fmt=' ', color='black', marker='x', ms=8, alpha=1)
plt.xticks(ticks=ring.locations(), labels=dict.fromkeys([name for name, kind, *_ in ring.layout() if kind == 'BPM']))
plt.tight_layout()
plt.show()
# Accuracy
print(qx - Qx)
print()
print(px - Px)
print()
print(qy - Qy)
print()
print(py - Py)
print()
tensor([ 1.0330e-03, -2.0600e-03, -8.5705e-05, -5.3725e-04],
dtype=torch.float64)
tensor([ 1.0330e-03, -2.0600e-03, -8.5705e-05, -5.3725e-04],
dtype=torch.float64)
True
tensor([ 0.0010, -0.0020, 0.0000, 0.0000], dtype=torch.float64)
tensor([ 0.0000e+00, 0.0000e+00, -8.9063e-05, -5.4190e-04],
dtype=torch.float64)




tensor([ 1.6464e-05, 1.1927e-05, -2.6803e-05, 1.7572e-05, 3.0857e-05,
-1.9706e-05, 3.3654e-06, 2.0557e-05, 1.1557e-05, -2.4882e-05,
1.7224e-05, -2.8642e-05, -1.6480e-05, 2.3818e-05, -2.5943e-05,
5.2350e-06], dtype=torch.float64)
tensor([-2.0294e-05, -2.9471e-05, -4.3883e-05, 3.7667e-05, -4.6071e-05,
2.2920e-05, 1.5767e-05, 3.0890e-05, -3.0656e-05, 4.0570e-05,
3.0196e-05, -4.2305e-05, 3.5224e-05, -4.0320e-05, -4.5387e-05,
2.0621e-05], dtype=torch.float64)
tensor([ 3.3573e-06, 2.4453e-07, -1.2019e-06, 3.9919e-06, 5.5643e-06,
-6.7395e-08, -1.5772e-06, -3.8644e-06, -4.6883e-07, 2.0518e-06,
3.9661e-06, 7.6349e-06, 1.8919e-06, -1.6691e-06, -7.2595e-07,
2.4373e-06], dtype=torch.float64)
tensor([ 4.6486e-06, -1.7863e-06, 4.3081e-06, -1.7264e-06, 5.2059e-06,
-2.0194e-06, 4.7156e-07, 6.3280e-06, 7.1448e-07, 4.2817e-06,
1.1039e-05, -1.0053e-05, -3.0277e-06, -1.5325e-06, 3.0609e-06,
-2.7708e-06], dtype=torch.float64)
[9]:
# Estimate center and spread at all BPM using direct tracking and MC sampling
# Note, epsilon should be None for vmap, convergence not checked
def fn(dx, dy):
guess = torch.tensor(4*[0.0], dtype=torch.float64)
point, _ = orbit(ring, guess, [dx, dy], ('dx', ['Quadrupole'], None, None), ('dy', ['Quadrupole'], None, None), alignment=True, advance=True, full=False, limit=16, epsilon=None)
return point
dxs = 50.0E-6*torch.randn((8192, n_quad), dtype=torch.float64)
dys = 50.0E-6*torch.randn((8192, n_quad), dtype=torch.float64)
cqxs, cpxs, cqys, cpys = torch.vmap(fn)(dxs, dys).swapaxes(0, -1)
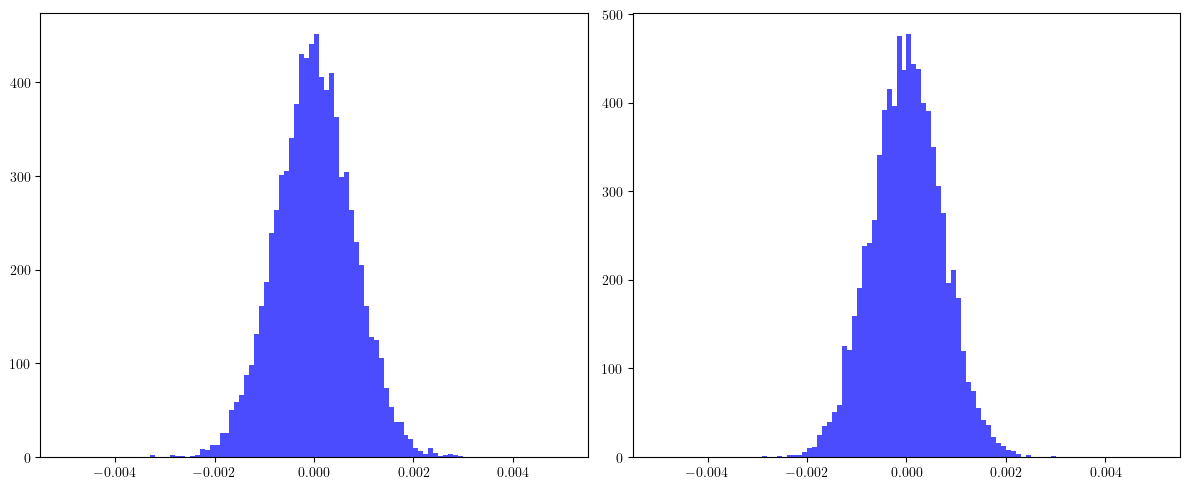
# Plot histogram at the first BPM for qx and qy
cqx, *_ = cqxs
cqy, *_ = cqys
fig, (ax, ay) = plt.subplots(1, 2, figsize=(12, 5))
ax.hist(cqx.cpu().numpy(), bins=100, range=(-5.0E-3, +5.0E-3), color='blue', alpha=0.7)
ay.hist(cqy.cpu().numpy(), bins=100, range=(-5.0E-3, +5.0E-3), color='blue', alpha=0.7)
plt.tight_layout()
plt.show()
# Estimate center and spread at all BPMs
qx_center_tracking = cqxs.mean(-1)
qy_center_tracking = cqys.mean(-1)
qx_spread_tracking = cqxs.std(-1)
qy_spread_tracking = cqys.std(-1)
[10]:
# Estimate spread (error propagation)
dx = torch.tensor(n_quad*[0.0], dtype=torch.float64)
dy = torch.tensor(n_quad*[0.0], dtype=torch.float64)
def fx(dx):
qx, px, qy, py = torch.stack([evaluate(local, [fp, dx]) for local in pox]).T
return qx
def fy(dy):
qx, px, qy, py = torch.stack([evaluate(local, [fp, dy]) for local in poy]).T
return qy
jx = torch.func.jacrev(fx)(dx)
jy = torch.func.jacrev(fy)(dy)
sx = 50.0E-6*torch.ones_like(dx)
sy = 50.0E-6*torch.ones_like(dy)
sx = torch.diag(sx**2)
sy = torch.diag(sy**2)
qx_spread_error = (jx @ sx @ jx.T).diag().sqrt()
qy_spread_error = (jy @ sy @ jy.T).diag().sqrt()
[11]:
# Plot (compare estimated spreads)
plt.figure(figsize=(16, 2))
plt.bar(range(len(ring.locations())), qx_spread_tracking.cpu().numpy(), color='blue',alpha=0.75)
plt.bar(range(len(ring.locations())), qx_spread_error.cpu().numpy(), color='red', alpha=0.50)
plt.xticks(ticks=range(len(ring.locations())), labels=dict.fromkeys([name for name, kind, *_ in ring.layout() if kind == 'BPM']))
plt.tight_layout()
plt.show()
plt.figure(figsize=(16, 2))
plt.bar(range(len(ring.locations())), qy_spread_tracking.cpu().numpy(), color='blue',alpha=0.75)
plt.bar(range(len(ring.locations())), qy_spread_error.cpu().numpy(), color='red', alpha=0.50)
plt.xticks(ticks=range(len(ring.locations())), labels=dict.fromkeys([name for name, kind, *_ in ring.layout() if kind == 'BPM']))
plt.tight_layout()
plt.show()


[12]:
# Estimate center and spread at all BPM using series and MC sampling
dxs = 50.0E-6*torch.randn((8192, n_quad), dtype=torch.float64)
dys = 50.0E-6*torch.randn((8192, n_quad), dtype=torch.float64)
cqxs, _, _, _ = torch.stack([torch.func.vmap(lambda dx: evaluate(local, [fp, dx]))(dxs) for local in pox]).swapaxes(0, -1)
_, _, cqys, _ = torch.stack([torch.func.vmap(lambda dy: evaluate(local, [fp, dy]))(dys) for local in poy]).swapaxes(0, -1)
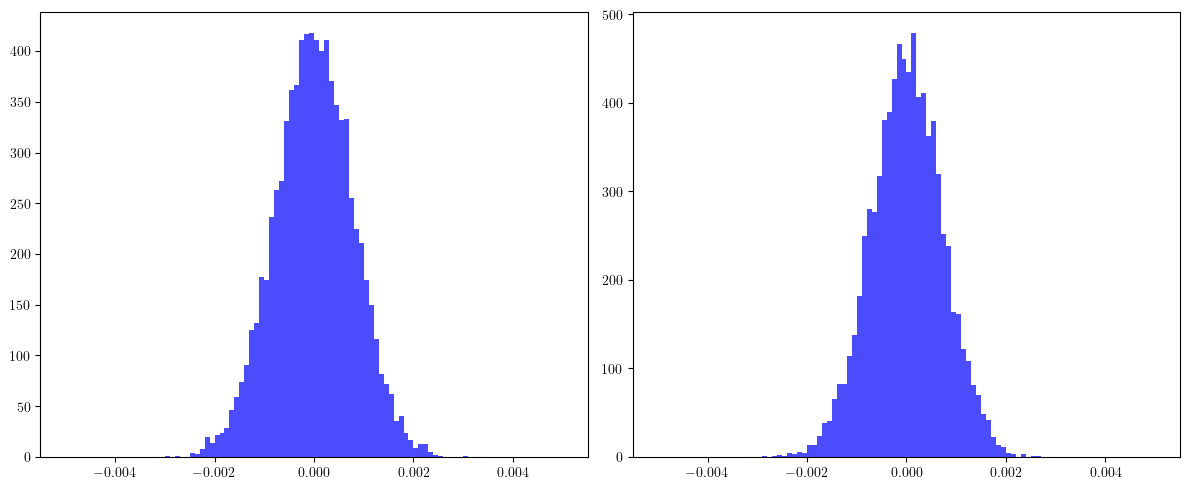
# Plot histogram at the first BPM for qx and qy
cqx, *_ = cqxs.T
cqy, *_ = cqys.T
fig, (ax, ay) = plt.subplots(1, 2, figsize=(12, 5))
ax.hist(cqx.cpu().numpy(), bins=100, range=(-5.0E-3, +5.0E-3), color='blue', alpha=0.7)
ay.hist(cqy.cpu().numpy(), bins=100, range=(-5.0E-3, +5.0E-3), color='blue', alpha=0.7)
plt.tight_layout()
plt.show()
# Estimate center and spread at all BPMs
qx_center_taylor = cqxs.T.mean(-1)
qy_center_taylor = cqys.T.mean(-1)
qx_spread_taylor = cqxs.T.std(-1)
qy_spread_taylor = cqys.T.std(-1)
[13]:
# Plot (compare estimated spreads)
plt.figure(figsize=(16, 2))
plt.bar(range(len(ring.locations())), qx_spread_tracking.cpu().numpy(), color='blue',alpha=0.75)
plt.bar(range(len(ring.locations())), qx_spread_taylor.cpu().numpy(), color='red', alpha=0.50)
plt.xticks(ticks=range(len(ring.locations())), labels=dict.fromkeys([name for name, kind, *_ in ring.layout() if kind == 'BPM']))
plt.tight_layout()
plt.show()
plt.figure(figsize=(16, 2))
plt.bar(range(len(ring.locations())), qy_spread_tracking.cpu().numpy(), color='blue',alpha=0.75)
plt.bar(range(len(ring.locations())), qy_spread_taylor.cpu().numpy(), color='red', alpha=0.50)
plt.xticks(ticks=range(len(ring.locations())), labels=dict.fromkeys([name for name, kind, *_ in ring.layout() if kind == 'BPM']))
plt.tight_layout()
plt.show()

