ELETTRA-06: ID tune shift correction (global tune knob)
[1]:
# In this example effects of an ID (APPLE-II device represented by a linear 4x4 symplectic matrix) are presented
# Tune shift introduced by ID is corrected using model tune response matrix
[2]:
# Import
import torch
from torch import Tensor
from pathlib import Path
import matplotlib
from matplotlib import pyplot as plt
from matplotlib.patches import Rectangle
matplotlib.rcParams['text.usetex'] = True
from model.library.element import Element
from model.library.line import Line
from model.library.quadrupole import Quadrupole
from model.library.matrix import Matrix
from model.command.external import load_lattice
from model.command.build import build
from model.command.tune import tune
from model.command.orbit import dispersion
from model.command.twiss import twiss
from model.command.advance import advance
from model.command.coupling import coupling
[3]:
# Set data type and device
Element.dtype = dtype = torch.float64
Element.device = device = torch.device('cpu')
[4]:
# Load lattice (ELEGANT table)
# Note, lattice is allowed to have repeated elements
path = Path('elettra.lte')
data = load_lattice(path)
[5]:
# Build and setup lattice
ring:Line = build('RING', 'ELEGANT', data)
# Flatten sublines
ring.flatten()
# Remove all marker elements but the ones starting with MLL (long straight section centers)
ring.remove_group(pattern=r'^(?!MLL_).*', kinds=['Marker'])
# Replace all sextupoles with quadrupoles
def factory(element:Element) -> None:
table = element.serialize
table.pop('ms', None)
return Quadrupole(**table)
ring.replace_group(pattern=r'', factory=factory, kinds=['Sextupole'])
# Set linear dipoles
def apply(element:Element) -> None:
element.linear = True
ring.apply(apply, kinds=['Dipole'])
# Merge drifts
ring.merge()
# Change lattice start
ring.start = "BPM_S01_01"
# Split BPMs
ring.split((None, ['BPM'], None, None))
# Roll lattice
ring.roll(1)
# Splice lattice
ring.splice()
# Describe
ring.describe
[5]:
{'BPM': 168, 'Drift': 708, 'Dipole': 156, 'Quadrupole': 360, 'Marker': 12}
[6]:
# Compute tunes (fractional part)
nux, nuy = tune(ring, [], matched=True, limit=1)
[7]:
# Compute dispersion
orbit = torch.tensor(4*[0.0], dtype=dtype)
etaqx, etapx, etaqy, etapy = dispersion(ring, orbit, [], limit=1)
[8]:
# Compute twiss parameters
ax, bx, ay, by = twiss(ring, [], matched=True, advance=True, full=False).T
[9]:
# Compute phase advances
mux, muy = advance(ring, [], alignment=False, matched=True).T
[10]:
# Compute coupling
c = coupling(ring, [])
[11]:
# Quadrupole names for global tune correction
QF = [f'QF_S{i:02}_{j:02}' for j in [2, 3] for i in range(1, 12 + 1)]
QD = [f'QD_S{i:02}_{j:02}' for j in [2, 3] for i in range(1, 12 + 1)]
[12]:
# Compute model tune response matrix
def observable(kn):
return tune(ring, [kn], ('kn', None, QF + QD, None), matched=True, limit=1)
kn = torch.zeros(len(QF + QD), dtype=torch.float64)
matrix = torch.func.jacrev(observable)(kn)
[13]:
# Define ID model
# Note, only the flattened triangular part of the A and B matrices is passed
A = torch.tensor([[-0.03484222052711237, 1.0272120741819959E-7, -4.698931299341201E-9, 0.0015923185492594811],
[1.0272120579834892E-7, -0.046082787920135176, 0.0017792061173117564, 3.3551298301095784E-8],
[-4.6989312853101E-9, 0.0017792061173117072, 0.056853750760983084, -1.5929605363332683E-7],
[0.0015923185492594336, 3.3551298348653296E-8, -1.5929605261642905E-7, 0.08311631737263032]], dtype=dtype)
B = torch.tensor([[0.03649353186115209, 0.0015448347221877217, 0.00002719892025520868, -0.0033681183134964482],
[0.0015448347221877217, 0.13683886657005795, -0.0033198692682377406, 0.00006140578258682469],
[0.00002719892025520868, -0.0033198692682377406, -0.05260095308967722, 0.005019907688182885],
[-0.0033681183134964482, 0.00006140578258682469, 0.005019907688182885, -0.2531573249456863]], dtype=dtype)
ID = Matrix('ID',
length=0.0,
A=A[torch.triu(torch.ones_like(A, dtype=torch.bool))].tolist(),
B=B[torch.triu(torch.ones_like(B, dtype=torch.bool))].tolist())
[14]:
# Insert ID into the existing lattice
# This will replace the target marker
ring.flatten()
ring.insert(ID, 'MLL_S01', position=0.0)
ring.splice()
# Describe
ring.describe
[14]:
{'BPM': 168,
'Drift': 708,
'Dipole': 156,
'Quadrupole': 360,
'Matrix': 1,
'Marker': 11}
[15]:
# Compute tunes (fractional part)
nux_id, nuy_id = tune(ring, [], matched=True, limit=1)
[16]:
# Compute dispersion
orbit = torch.tensor(4*[0.0], dtype=dtype)
etaqx_id, etapx_id, etaqy_id, etapy_id = dispersion(ring, orbit, [], limit=1)
[17]:
# Compute twiss parameters
ax_id, bx_id, ay_id, by_id = twiss(ring, [], matched=True, advance=True, full=False).T
[18]:
# Compute phase advances
mux_id, muy_id = advance(ring, [], alignment=False, matched=True).T
[19]:
# Compute coupling
c_id = coupling(ring, [])
[20]:
# Parametric tunes (emulate tune measurement)
def observable(kn):
return tune(ring, [kn], ('kn', None, QF + QD, None), matched=True, limit=1)
[21]:
# Tune correction
# Observe tunes for lattice with errors (inserted ID) while adjusting quadrupoles using model response matrix
# With this method the ID model is not required, but several rounds of observable measurement are performed
lr = 0.75
kn = torch.zeros(len(QF + QD), dtype=torch.float64)
target = torch.stack([nux, nuy])
for _ in range(16):
value = observable(kn)
kn -= lr*torch.linalg.lstsq(matrix, value - target, driver='gels').solution
print((value - target).norm())
print()
tensor(0.0284, dtype=torch.float64)
tensor(0.0067, dtype=torch.float64)
tensor(0.0016, dtype=torch.float64)
tensor(0.0004, dtype=torch.float64)
tensor(9.4026e-05, dtype=torch.float64)
tensor(2.2813e-05, dtype=torch.float64)
tensor(5.5475e-06, dtype=torch.float64)
tensor(1.3520e-06, dtype=torch.float64)
tensor(3.3015e-07, dtype=torch.float64)
tensor(8.0778e-08, dtype=torch.float64)
tensor(1.9800e-08, dtype=torch.float64)
tensor(4.8613e-09, dtype=torch.float64)
tensor(1.1954e-09, dtype=torch.float64)
tensor(2.9439e-10, dtype=torch.float64)
tensor(7.2593e-11, dtype=torch.float64)
tensor(1.7923e-11, dtype=torch.float64)
[22]:
# Apply corrections
ring.flatten()
for name, value in zip(QF + QD, kn):
ring[name].kn = (ring[name].kn + value).item()
ring.splice()
[23]:
# Compute tunes (fractional part)
nux_c, nuy_c = tune(ring, [], matched=True, limit=1)
[24]:
# Compute dispersion
orbit = torch.tensor(4*[0.0], dtype=dtype)
etaqx_c, etapx_c, etaqy_c, etapy_c = dispersion(ring, orbit, [], limit=1)
[25]:
# Compute twiss parameters
ax_c, bx_c, ay_c, by_c = twiss(ring, [], matched=True, advance=True, full=False).T
[26]:
# Compute phase advances
mux_c, muy_c = advance(ring, [], alignment=False, matched=True).T
[27]:
# Compute coupling
c_c = coupling(ring, [])
[28]:
# Tune shifts
print((nux - nux_id).abs())
print((nuy - nuy_id).abs())
print()
print((nux - nux_c).abs())
print((nuy - nuy_c).abs())
print()
tensor(0.0260, dtype=torch.float64)
tensor(0.0114, dtype=torch.float64)
tensor(3.2221e-12, dtype=torch.float64)
tensor(3.0445e-12, dtype=torch.float64)
[29]:
# Coupling (minimal tune distance)
print(c)
print(c_id)
print(c_c)
tensor(0., dtype=torch.float64)
tensor(0.0004, dtype=torch.float64)
tensor(0.0004, dtype=torch.float64)
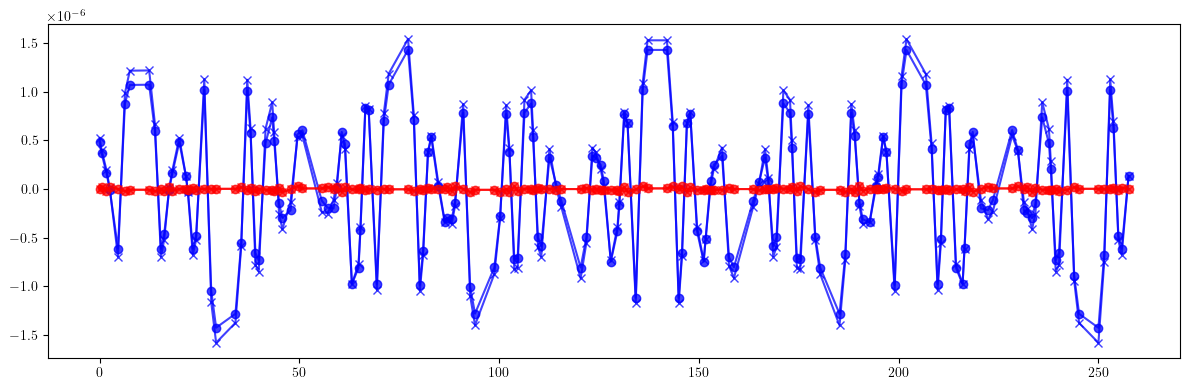
[30]:
# Dispersion
plt.figure(figsize=(12, 4))
plt.errorbar(ring.locations().cpu().numpy(), (etaqx - etaqx_id).cpu().numpy(), fmt='-', marker='x', color='blue', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), (etaqy - etaqy_id).cpu().numpy(), fmt='-', marker='x', color='red', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), (etaqx - etaqx_c).cpu().numpy(), fmt='-', marker='o', color='blue', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), (etaqy - etaqy_c).cpu().numpy(), fmt='-', marker='o', color='red', alpha=0.75)
plt.tight_layout()
plt.show()
print(((etaqx - etaqx_id)**2).mean().sqrt(), (etaqx - etaqx_id).max() - (etaqx - etaqx_id).min())
print(((etaqy - etaqy_id)**2).mean().sqrt(), (etaqy - etaqy_id).max() - (etaqy - etaqy_id).min())
print()
print(((etaqx - etaqx_c)**2).mean().sqrt(), (etaqx - etaqx_c).max() - (etaqx - etaqx_c).min())
print(((etaqy - etaqy_c)**2).mean().sqrt(), (etaqy - etaqy_c).max() - (etaqy - etaqy_c).min())
print()
tensor(7.4928e-07, dtype=torch.float64) tensor(3.1227e-06, dtype=torch.float64)
tensor(1.4168e-08, dtype=torch.float64) tensor(6.0573e-08, dtype=torch.float64)
tensor(6.8912e-07, dtype=torch.float64) tensor(2.8567e-06, dtype=torch.float64)
tensor(1.4789e-08, dtype=torch.float64) tensor(6.3260e-08, dtype=torch.float64)
[31]:
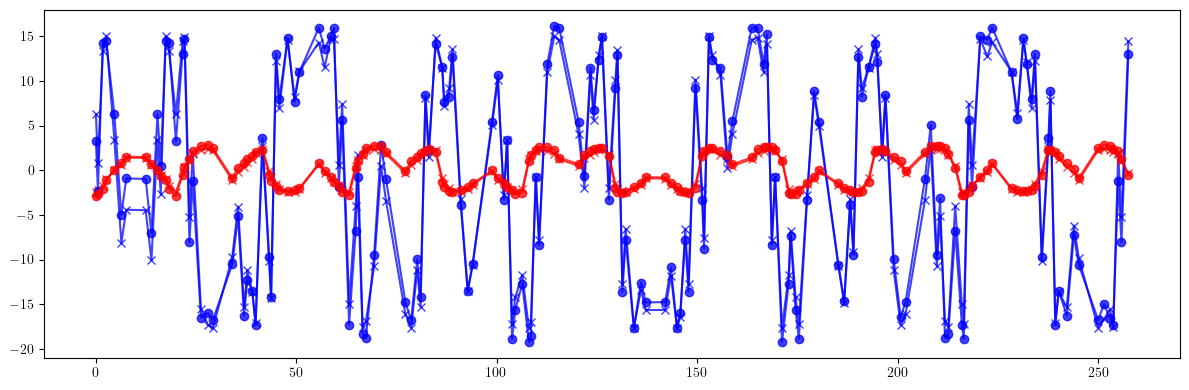
# Beta-beating
plt.figure(figsize=(12, 4))
plt.errorbar(ring.locations().cpu().numpy(), 100*((bx - bx_id)/bx).cpu().numpy(), fmt='-', marker='x', color='blue', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), 100*((by - by_id)/by).cpu().numpy(), fmt='-', marker='x', color='red', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), 100*((bx - bx_c)/bx).cpu().numpy(), fmt='-', marker='o', color='blue', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), 100*((by - by_c)/by).cpu().numpy(), fmt='-', marker='o', color='red', alpha=0.75)
plt.tight_layout()
plt.show()
print(100*(((bx - bx_id)/bx)**2).mean().sqrt(), 100*(((bx - bx_id)/bx).max() - ((bx - bx_id)/bx).min()))
print(100*(((by - by_id)/by)**2).mean().sqrt(), 100*(((by - by_id)/by).max() - ((by - by_id)/by).min()))
print()
print(100*(((bx - bx_c)/bx)**2).mean().sqrt(), 100*(((bx - bx_c)/bx).max() - ((bx - bx_c)/bx).min()))
print(100*(((by - by_c)/by)**2).mean().sqrt(), 100*(((by - by_c)/by).max() - ((by - by_c)/by).min()))
print()
tensor(11.5994, dtype=torch.float64) tensor(32.6569, dtype=torch.float64)
tensor(1.7916, dtype=torch.float64) tensor(4.8154, dtype=torch.float64)
tensor(11.8471, dtype=torch.float64) tensor(35.3888, dtype=torch.float64)
tensor(1.9331, dtype=torch.float64) tensor(5.7332, dtype=torch.float64)
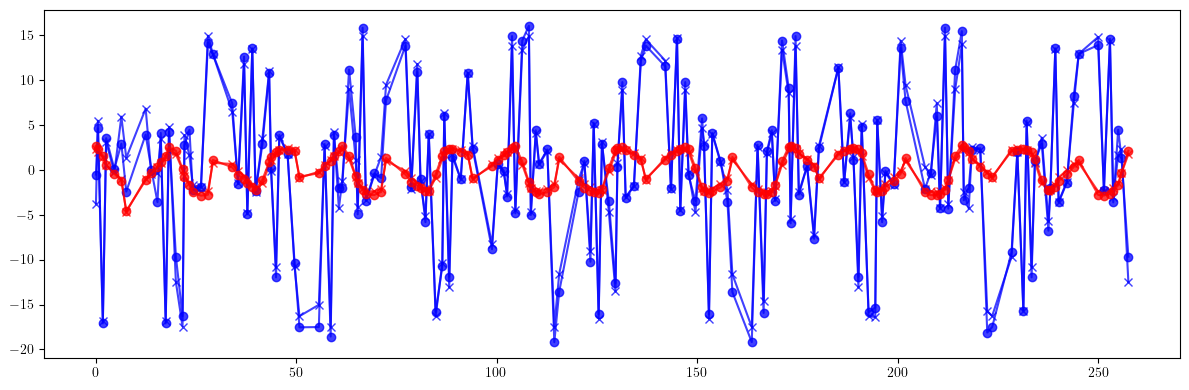
[32]:
# Phase advance
plt.figure(figsize=(12, 4))
plt.errorbar(ring.locations().cpu().numpy(), 100*((mux - mux_id)/mux).cpu().numpy(), fmt='-', marker='x', color='blue', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), 100*((muy - muy_id)/muy).cpu().numpy(), fmt='-', marker='x', color='red', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), 100*((mux - mux_c)/mux).cpu().numpy(), fmt='-', marker='o', color='blue', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), 100*((muy - muy_c)/muy).cpu().numpy(), fmt='-', marker='o', color='red', alpha=0.75)
plt.tight_layout()
plt.show()
print(100*(((mux - mux_id)/mux)**2).mean().sqrt(), 100*(((mux - mux_id)/mux).max() - ((mux - mux_id)/mux).min()))
print(100*(((muy - muy_id)/muy)**2).mean().sqrt(), 100*(((muy - muy_id)/muy).max() - ((muy - muy_id)/muy).min()))
print()
print(100*(((mux - mux_c)/mux)**2).mean().sqrt(), 100*(((mux - mux_c)/mux).max() - ((mux - mux_c)/mux).min()))
print(100*(((muy - muy_c)/muy)**2).mean().sqrt(), 100*(((muy - muy_c)/muy).max() - ((muy - muy_c)/muy).min()))
print()
tensor(8.7941, dtype=torch.float64) tensor(32.4432, dtype=torch.float64)
tensor(1.7778, dtype=torch.float64) tensor(7.0609, dtype=torch.float64)
tensor(8.9663, dtype=torch.float64) tensor(35.2147, dtype=torch.float64)
tensor(1.9193, dtype=torch.float64) tensor(7.3238, dtype=torch.float64)