ELETTRA-07: ID tune shift fit & correction (global tune knob)

# In this example effects of an ID (APPLE-II device represented by a linear 4x4 symplectic matrix) are presented

# Tune shift introduced by ID is first used to fit the ID model
# Next, global tune correction is performed using the fitted model and the correction result is evaluated

# Import

import torch
from torch import Tensor

from pathlib import Path

import matplotlib
from matplotlib import pyplot as plt
from matplotlib.patches import Rectangle
matplotlib.rcParams['text.usetex'] = True

from model.library.element import Element
from model.library.line import Line
from model.library.quadrupole import Quadrupole
from model.library.matrix import Matrix

from model.command.external import load_lattice
from model.command.build import build
from model.command.tune import tune
from model.command.orbit import dispersion
from model.command.twiss import twiss
from model.command.advance import advance
from model.command.coupling import coupling

from model.command.wrapper import Wrapper

# Set data type and device

Element.dtype = dtype = torch.float64
Element.device = device = torch.device('cpu')

# Load lattice (ELEGANT table)
# Note, lattice is allowed to have repeated elements

path = Path('elettra.lte')
data = load_lattice(path)

# Build and setup lattice

ring:Line = build('RING', 'ELEGANT', data)

# Flatten sublines

ring.flatten()

# Remove all marker elements but the ones starting with MLL (long straight section centers)

ring.remove_group(pattern=r'^(?!MLL_).*', kinds=['Marker'])

# Replace all sextupoles with quadrupoles

def factory(element:Element) -> None:
    table = element.serialize
    table.pop('ms', None)
    return Quadrupole(**table)

ring.replace_group(pattern=r'', factory=factory, kinds=['Sextupole'])

# Set linear dipoles

def apply(element:Element) -> None:
    element.linear = True

ring.apply(apply, kinds=['Dipole'])

# Merge drifts

ring.merge()

# Change lattice start

ring.start = "BPM_S01_01"

# Split BPMs

ring.split((None, ['BPM'], None, None))

# Roll lattice

ring.roll(1)

# Splice lattice

ring.splice()

# Describe

ring.describe

{'BPM': 168, 'Drift': 708, 'Dipole': 156, 'Quadrupole': 360, 'Marker': 12}

# Compute tunes (fractional part)

nux, nuy = tune(ring, [], matched=True, limit=1)

# Compute dispersion

orbit = torch.tensor(4*[0.0], dtype=dtype)
etaqx, etapx, etaqy, etapy = dispersion(ring, orbit, [], limit=1)

# Compute twiss parameters

ax, bx, ay, by = twiss(ring, [], matched=True, advance=True, full=False).T

# Compute phase advances

mux, muy = advance(ring, [], alignment=False, matched=True).T

# Compute coupling

c = coupling(ring, [])

# Define ID model
# Note, only the flattened triangular part of the A and B matrices is passed

A = torch.tensor([[-0.03484222052711237, 1.0272120741819959E-7, -4.698931299341201E-9, 0.0015923185492594811],
                  [1.0272120579834892E-7, -0.046082787920135176, 0.0017792061173117564, 3.3551298301095784E-8],
                  [-4.6989312853101E-9, 0.0017792061173117072, 0.056853750760983084, -1.5929605363332683E-7],
                  [0.0015923185492594336, 3.3551298348653296E-8, -1.5929605261642905E-7, 0.08311631737263032]], dtype=dtype)

B = torch.tensor([[0.03649353186115209, 0.0015448347221877217, 0.00002719892025520868, -0.0033681183134964482],
                  [0.0015448347221877217, 0.13683886657005795, -0.0033198692682377406, 0.00006140578258682469],
                  [0.00002719892025520868, -0.0033198692682377406, -0.05260095308967722, 0.005019907688182885],
                  [-0.0033681183134964482, 0.00006140578258682469, 0.005019907688182885, -0.2531573249456863]], dtype=dtype)

ID = Matrix('ID',
            length=0.0,
            A=A[torch.triu(torch.ones_like(A, dtype=torch.bool))].tolist(),
            B=B[torch.triu(torch.ones_like(B, dtype=torch.bool))].tolist())

# Insert ID into the existing lattice
# This will replace the target marker

error = ring.clone()
error.flatten()
error.insert(ID, 'MLL_S01', position=0.0)
error.splice()

# Measure tunes with ID

nux_id, nuy_id = target = tune(error, [], matched=True)

print((nux - nux_id).abs())
print((nuy - nuy_id).abs())

tensor(0.0260, dtype=torch.float64)
tensor(0.0114, dtype=torch.float64)

# Compute dispersion

orbit = torch.tensor(4*[0.0], dtype=dtype)
etaqx_id, etapx_id, etaqy_id, etapy_id = dispersion(error, orbit, [], limit=1)

# Compute twiss parameters

ax_id, bx_id, ay_id, by_id = twiss(error, [], matched=True, advance=True, full=False).T

# Compute phase advances

mux_id, muy_id = advance(error, [], alignment=False, matched=True).T

# Compute coupling

c_id = coupling(error, [])

# Create a ring with ID to be fitted to measured observables (tunes)

TM = Matrix('TM')

model = ring.clone()
model.flatten()
model.insert(TM, 'MLL_S01', position=0.0)
model.splice()

# Define parametric observable

def observable(knobs):
    a11, a12, a13, a14, a22, a23, a24, a33, a34, a44 = knobs.reshape(-1, 1)
    return tune(model,
                [a11, a12, a13, a14, a22, a23, a24, a33, a34, a44],
                ('a11', None, ['TM'], None),
                ('a12', None, ['TM'], None),
                ('a13', None, ['TM'], None),
                ('a14', None, ['TM'], None),
                ('a22', None, ['TM'], None),
                ('a23', None, ['TM'], None),
                ('a24', None, ['TM'], None),
                ('a33', None, ['TM'], None),
                ('a34', None, ['TM'], None),
                ('a44', None, ['TM'], None),
                matched=True)

# Test observable with known ID model

print(target)
print(observable(ID.A))

tensor([0.2735, 0.1723], dtype=torch.float64)
tensor([0.2735, 0.1723], dtype=torch.float64)

# Define objective function to be fitted

def objective(knobs):
    return ((target - observable(knobs))**2).sum()

print(objective(0.0*ID.A))
print(objective(1.0*ID.A))

tensor(0.0008, dtype=torch.float64)
tensor(0., dtype=torch.float64)

# Fit (ADAM)

knobs = torch.tensor(10*[0.0], dtype=dtype)

wrapper = Wrapper(objective, knobs)
optimizer = torch.optim.AdamW(wrapper.parameters(), lr=0.001)
scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=32, gamma=0.95)

for epoch in range(256):
    value = wrapper()
    value.backward()
    optimizer.step()
    optimizer.zero_grad()
    scheduler.step()
    print(value.detach().item())

0.0008048399068028212
0.0007620349342060703
0.0007205307248509358
0.0006803424125036658
0.0006414829893953095
0.000603963179617447
0.0005677915620312731
0.0005329731984290826
0.0004995122939169441
0.0004674085174248959
0.0004366601056032604
0.0004072621312454616
0.0003792063439073972
0.00035248203582205717
0.0003270757300961398
0.0003029708127255459
0.0002801477863792213
0.0002585845600949164
0.00023825635953760388
0.00021913568060475866
0.0002011924927164019
0.00018439447901961084
0.00016870714114430743
0.00015409389745957427
0.00014051628793088745
0.00012793422756922452
0.00011630622031845724
0.00010558955674398206
9.574054947860015e-05
8.67147997185777e-05
7.846745200867355e-05
7.095343221204984e-05
6.412769310437521e-05
5.8244372091230745e-05
5.2910475720096975e-05
4.808632410942108e-05
4.373340605244055e-05
3.981449880451027e-05
3.6293785401960895e-05
3.3136958575082696e-05
3.031130622646868e-05
2.778578191273694e-05
2.553106407645505e-05
2.351960251849228e-05
2.1725647947110543e-05
2.012526316349036e-05
1.8696318148762623e-05
1.7418471779002293e-05
1.6273140899374286e-05
1.5243456219811562e-05
1.4314205333691484e-05
1.3471764748346206e-05
1.2704023374310251e-05
1.2000299290200252e-05
1.1351250843166973e-05
1.074878306475984e-05
1.0185950827475094e-05
9.656860495384129e-06
9.156571696318549e-06
8.681000443233331e-06
8.226824510679523e-06
7.791391879612098e-06
7.372633090077241e-06
6.968978139267706e-06
6.579279594350578e-06
6.221246569114974e-06
5.874584748473645e-06
5.5390357044105244e-06
5.214500571610839e-06
4.900996688150615e-06
4.598619969033483e-06
4.307512749930254e-06
4.027836779773489e-06
3.7597509995008677e-06
3.503393722740693e-06
3.258868826017142e-06
3.0262355542054893e-06
2.80550154690835e-06
2.5966186934312645e-06
2.399481430058305e-06
2.2139271049260698e-06
2.039738053472807e-06
1.876645049596499e-06
1.7243318230027e-06
1.5824403599514112e-06
1.4505767322925347e-06
1.328317227626482e-06
1.215214581879047e-06
1.1108041441697994e-06
1.014609832127314e-06
9.261497634617609e-07
8.449414756945979e-07
7.705066701762233e-07
7.023754384218696e-07
6.4008994796074e-07
5.832075814892246e-07
5.313035367880133e-07
4.862756633094264e-07
4.451054400468193e-07
4.074618259008803e-07
3.730366268395838e-07
3.41544310190802e-07
3.1272158241887614e-07
2.863267610803841e-07
2.621389706763429e-07
2.3995719109269305e-07
2.1959918632987406e-07
2.009003403926331e-07
1.837124263858768e-07
1.6790233413723542e-07
1.533507805502872e-07
1.3995102559602529e-07
1.2760761494239617e-07
1.1623516795252144e-07
1.0575722695875901e-07
9.610518067051083e-08
8.721727128618509e-08
7.903769163557492e-08
7.151577556029667e-08
6.460528193616114e-08
5.8263770277070013e-08
5.245206386077858e-08
4.7133794747689096e-08
4.227502393251919e-08
3.7843929145319366e-08
3.381055246391623e-08
3.0146599831051255e-08
2.68252847612967e-08
2.382120890295381e-08
2.124189250518132e-08
1.8911705432630753e-08
1.6810707695301007e-08
1.4920119209947974e-08
1.322227135462331e-08
1.1700566863789782e-08
1.0339445336516158e-08
9.124352148723321e-09
8.041709015266836e-09
7.078884858034939e-09
6.224165997579924e-09
5.46672500173781e-09
4.7965877836622755e-09
4.204598771074889e-09
3.6823841485531696e-09
3.222313314825974e-09
2.8174588098937067e-09
2.4615550467762923e-09
2.148956229995865e-09
1.874593873461849e-09
1.633934339393752e-09
1.4229368076802283e-09
1.2380120660374654e-09
1.075982475515269e-09
9.34043427770928e-10
8.097265619927811e-10
7.008649629509901e-10
6.055605093182176e-10
5.221534937153706e-10
4.491945878415242e-10
3.854191821333239e-10
3.2972408830518954e-10
2.834815510603664e-10
2.4302892976403254e-10
2.0769278275067256e-10
1.7688388787835946e-10
1.500851674955018e-10
1.26841280905522e-10
1.067497201164048e-10
8.945324771219374e-11
7.463352166598677e-11
6.200575757354876e-11
5.1314289166859826e-11
4.23288968110366e-11
3.484178487909292e-11
2.866509986918011e-11
2.3628893176730483e-11
1.9579443106838884e-11
1.637786242288806e-11
1.3898928264842267e-11
1.2030081182733315e-11
1.0670549600046278e-11
9.73056429240154e-12
9.130635305340482e-12
8.800870259396595e-12
8.680318959797025e-12
8.716334018483965e-12
8.86394146032254e-12
9.0852183214561e-12
9.348677136551794e-12
9.628658787066918e-12
9.9047367670138e-12
1.016113659120617e-11
1.038617451822745e-11
1.0562159079872892e-11
1.0695560714543745e-11
1.0784318295856108e-11
1.082825842949763e-11
1.0828724659145301e-11
1.0788243651508464e-11
1.0710228217031282e-11
1.0598716507445306e-11
1.0458146129027407e-11
1.0293161660647792e-11
1.0108453670744687e-11
9.908626958105299e-12
9.698095694137904e-12
9.481002789420563e-12
9.261161016383427e-12
9.042013112892124e-12
8.826608340806471e-12
8.617592953065961e-12
8.417212247492623e-12
8.227321896766784e-12
8.04940658591718e-12
7.884604103376039e-12
7.73373320378322e-12
7.597323908899757e-12
7.475648928767757e-12
7.368755281110631e-12
7.276495238344267e-12
7.198555960686624e-12
7.1344873516487256e-12
7.083727776870241e-12
7.045627448527154e-12
7.019469350428524e-12
7.005151783481877e-12
7.000508841404414e-12
7.004766837513574e-12
7.017151902628571e-12
7.036897536924574e-12
7.0632507303902056e-12
7.095476882743043e-12
7.132863601822149e-12
7.174723650169655e-12
7.220397126695855e-12
7.269253018257456e-12
7.320690290286747e-12
7.374138563353008e-12
7.429058528871547e-12
7.484942084717563e-12
7.541312361985461e-12
7.597723576474362e-12
7.653760820429717e-12
7.709039784255273e-12
7.763206398582717e-12
7.815936461915548e-12
7.866935203597298e-12
7.915936783831684e-12
7.962703792642061e-12
8.007026653793348e-12
8.048722935172925e-12
8.087636697902725e-12
8.12363763670515e-12
8.156620256984968e-12
8.186502899229477e-12
8.213226744660305e-12

# Fit (LBFGS)

knobs = torch.tensor(10*[0.0], dtype=dtype, requires_grad=True)
optimizer = torch.optim.LBFGS([knobs], lr=0.1, line_search_fn="strong_wolfe")

def closure():
    optimizer.zero_grad()
    value = objective(knobs)
    value.backward()
    return value

for epoch in range(8):
    value = optimizer.step(closure)
    print(value.item())

0.0008048399068028212
6.976747029574662e-11
6.976747029574662e-11
6.976747029574662e-11
6.976747029574662e-11
6.976747029574662e-11
6.976747029574662e-11
6.976747029574662e-11

# Check fitted tunes

print(target)
print(observable(ID.A))
print(observable(knobs.detach()))
print()

print((target - observable(ID.A)).abs())
print((target - observable(knobs.detach())).abs())

tensor([0.2735, 0.1723], dtype=torch.float64)
tensor([0.2735, 0.1723], dtype=torch.float64)
tensor([0.2735, 0.1723], dtype=torch.float64)

tensor([0., 0.], dtype=torch.float64)
tensor([6.7254e-07, 8.3256e-06], dtype=torch.float64)

# Define fitted model

TM.A = knobs.detach()

print(target)
print(tune(model, [], matched=True, limit=1))

tensor([0.2735, 0.1723], dtype=torch.float64)
tensor([0.2735, 0.1723], dtype=torch.float64)

# Define target tunes

target = tune(ring, [], matched=True, limit=1)
print(target)

tensor([0.2994, 0.1608], dtype=torch.float64)

# Define parametric observable

QF = [f'QF_S{i:02}_{j:02}' for j in [2, 3] for i in range(1, 12 + 1)]
QD = [f'QD_S{i:02}_{j:02}' for j in [2, 3] for i in range(1, 12 + 1)]

def observable(kn):
    return tune(model, [kn], ('kn', None, QF + QD, None), matched=True, limit=1)

knobs = torch.zeros(len(QF + QD), dtype=dtype)
print(observable(knobs))

tensor([0.2735, 0.1723], dtype=torch.float64)

# Define objective

def objective(knobs):
    return ((target - observable(knobs))**2).sum()

print(objective(knobs))

tensor(0.0008, dtype=torch.float64)

# Fit

knobs = torch.tensor(len(QF + QD)*[0.0], dtype=dtype, requires_grad=True)
optimizer = torch.optim.LBFGS([knobs], lr=0.1, line_search_fn="strong_wolfe")

def closure():
    optimizer.zero_grad()
    value = objective(knobs)
    value.backward()
    return value

for epoch in range(8):
    value = optimizer.step(closure)
    print(value.item())

0.0008049953927670922
4.915507721072069e-12
4.915507721072069e-12
4.915507721072069e-12
4.915507721072069e-12
4.915507721072069e-12
4.915507721072069e-12
4.915507721072069e-12

# Apply corrections to model with the exact ID

result = error.clone()
result.flatten()
for name, knob in zip(QF + QD, knobs.detach()):
    result[name].kn = (result[name].kn + knob).item()
result.splice()

# Compute tunes (fractional part)

nux_result, nuy_result = tune(result, [], matched=True, limit=1)

# Compute dispersion

orbit = torch.tensor(4*[0.0], dtype=dtype)
etaqx_result, etapx_result, etaqy_result, etapy_result = dispersion(result, orbit, [], limit=1)

# Compute twiss parameters

ax_result, bx_result, ay_result, by_result = twiss(result, [], matched=True, advance=True, full=False).T

# Compute phase advances

mux_result, muy_result = advance(result, [], alignment=False, matched=True).T

# Compute coupling

c_result = coupling(result, [])

# Tune shifts

print((nux - nux_id).abs())
print((nuy - nuy_id).abs())
print()

print((nux - nux_result).abs())
print((nuy - nuy_result).abs())
print()

tensor(0.0260, dtype=torch.float64)
tensor(0.0114, dtype=torch.float64)

tensor(0.0001, dtype=torch.float64)
tensor(0.0001, dtype=torch.float64)

# Coupling (minimal tune distance)

print(c)
print(c_id)
print(c_result)

tensor(0., dtype=torch.float64)
tensor(0.0004, dtype=torch.float64)
tensor(0.0003, dtype=torch.float64)

# Dispersion

plt.figure(figsize=(12, 4))
plt.errorbar(ring.locations().cpu().numpy(), (etaqx - etaqx_id).cpu().numpy(), fmt='-', marker='x', color='blue', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), (etaqy - etaqy_id).cpu().numpy(), fmt='-', marker='x', color='red', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), (etaqx - etaqx_result).cpu().numpy(), fmt='-', marker='o', color='blue', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), (etaqy - etaqy_result).cpu().numpy(), fmt='-', marker='o', color='red', alpha=0.75)

plt.tight_layout()
plt.show()

print(((etaqx - etaqx_id)**2).mean().sqrt(), (etaqx - etaqx_id).max() - (etaqx - etaqx_id).min())
print(((etaqy - etaqy_id)**2).mean().sqrt(), (etaqy - etaqy_id).max() - (etaqy - etaqy_id).min())
print()

print(((etaqx - etaqx_result)**2).mean().sqrt(), (etaqx - etaqx_result).max() - (etaqx - etaqx_result).min())
print(((etaqy - etaqy_result)**2).mean().sqrt(), (etaqy - etaqy_result).max() - (etaqy - etaqy_result).min())
print()

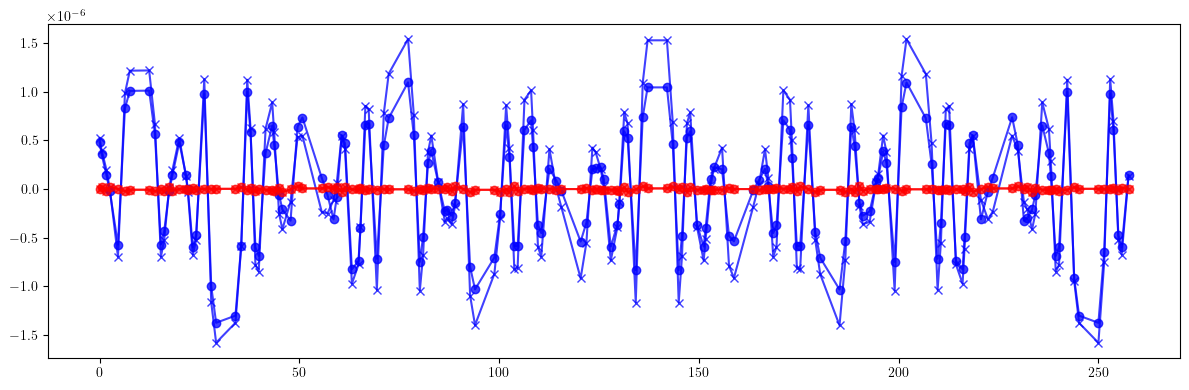
tensor(7.4928e-07, dtype=torch.float64) tensor(3.1227e-06, dtype=torch.float64)
tensor(1.4168e-08, dtype=torch.float64) tensor(6.0573e-08, dtype=torch.float64)

tensor(5.7138e-07, dtype=torch.float64) tensor(2.4011e-06, dtype=torch.float64)
tensor(1.4374e-08, dtype=torch.float64) tensor(6.1571e-08, dtype=torch.float64)

# Beta-beating

plt.figure(figsize=(12, 4))
plt.errorbar(ring.locations().cpu().numpy(), 100*((bx - bx_id)/bx).cpu().numpy(), fmt='-', marker='x', color='blue', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), 100*((by - by_id)/by).cpu().numpy(), fmt='-', marker='x', color='red', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), 100*((bx - bx_result)/bx).cpu().numpy(), fmt='-', marker='o', color='blue', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), 100*((by - by_result)/by).cpu().numpy(), fmt='-', marker='o', color='red', alpha=0.75)
plt.tight_layout()
plt.show()

print(100*(((bx - bx_id)/bx)**2).mean().sqrt(), 100*(((bx - bx_id)/bx).max() - ((bx - bx_id)/bx).min()))
print(100*(((by - by_id)/by)**2).mean().sqrt(), 100*(((by - by_id)/by).max() - ((by - by_id)/by).min()))
print()

print(100*(((bx - bx_result)/bx)**2).mean().sqrt(), 100*(((bx - bx_result)/bx).max() - ((bx - bx_result)/bx).min()))
print(100*(((by - by_result)/by)**2).mean().sqrt(), 100*(((by - by_result)/by).max() - ((by - by_result)/by).min()))
print()

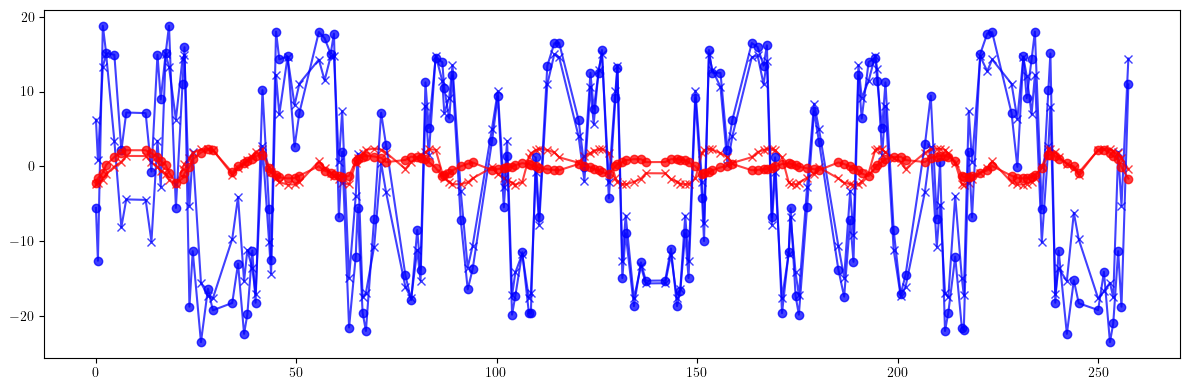
tensor(11.5994, dtype=torch.float64) tensor(32.6569, dtype=torch.float64)
tensor(1.7916, dtype=torch.float64) tensor(4.8154, dtype=torch.float64)

tensor(13.2856, dtype=torch.float64) tensor(41.9470, dtype=torch.float64)
tensor(1.0639, dtype=torch.float64) tensor(4.4647, dtype=torch.float64)

# Phase advance

plt.figure(figsize=(12, 4))
plt.errorbar(ring.locations().cpu().numpy(), 100*((mux - mux_id)/mux).cpu().numpy(), fmt='-', marker='x', color='blue', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), 100*((muy - muy_id)/muy).cpu().numpy(), fmt='-', marker='x', color='red', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), 100*((mux - mux_result)/mux).cpu().numpy(), fmt='-', marker='o', color='blue', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), 100*((muy - muy_result)/muy).cpu().numpy(), fmt='-', marker='o', color='red', alpha=0.75)
plt.tight_layout()
plt.show()

print(100*(((mux - mux_id)/mux)**2).mean().sqrt(), 100*(((mux - mux_id)/mux).max() - ((mux - mux_id)/mux).min()))
print(100*(((muy - muy_id)/muy)**2).mean().sqrt(), 100*(((muy - muy_id)/muy).max() - ((muy - muy_id)/muy).min()))
print()

print(100*(((mux - mux_result)/mux)**2).mean().sqrt(), 100*(((mux - mux_result)/mux).max() - ((mux - mux_result)/mux).min()))
print(100*(((muy - muy_result)/muy)**2).mean().sqrt(), 100*(((muy - muy_result)/muy).max() - ((muy - muy_result)/muy).min()))
print()

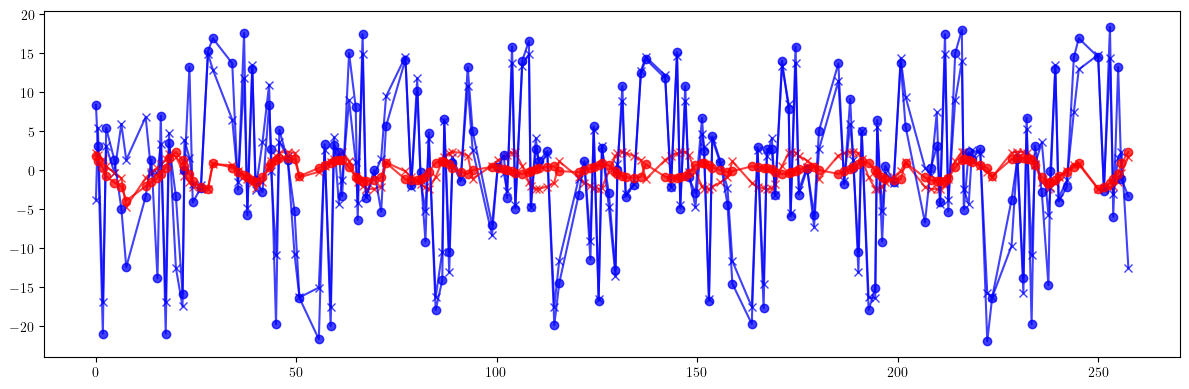
tensor(8.7941, dtype=torch.float64) tensor(32.4432, dtype=torch.float64)
tensor(1.7778, dtype=torch.float64) tensor(7.0609, dtype=torch.float64)

tensor(9.8962, dtype=torch.float64) tensor(39.6465, dtype=torch.float64)
tensor(1.0777, dtype=torch.float64) tensor(6.2230, dtype=torch.float64)