ELETTRA-21: ID model fit (symmetric: ORM & knobs utilization)
[1]:
# Import
import torch
from torch import Tensor
from pathlib import Path
import matplotlib
from matplotlib import pyplot as plt
from matplotlib.patches import Rectangle
matplotlib.rcParams['text.usetex'] = True
from model.library.element import Element
from model.library.line import Line
from model.library.corrector import Corrector
from model.library.quadrupole import Quadrupole
from model.library.matrix import Matrix
from model.command.external import load_lattice
from model.command.build import build
from model.command.tune import tune
from model.command.orbit import dispersion
from model.command.orbit import ORM
from model.command.twiss import twiss
from model.command.advance import advance
from model.command.coupling import coupling
from model.command.wrapper import Wrapper
from model.command.wrapper import forward
from model.command.wrapper import inverse
from model.command.wrapper import normalize
[2]:
# Set data type and device
Element.dtype = dtype = torch.float64
Element.device = device = torch.device('cpu')
[3]:
# Load lattice (ELEGANT table)
# Note, lattice is allowed to have repeated elements
path = Path('elettra.lte')
data = load_lattice(path)
[4]:
# Build and setup lattice
ring:Line = build('RING', 'ELEGANT', data)
# Flatten sublines
ring.flatten()
# Remove all marker elements but the ones starting with MLL (long straight section centers)
ring.remove_group(pattern=r'^(?!MLL_).*', kinds=['Marker'])
# Replace all sextupoles with quadrupoles
def factory(element:Element) -> None:
table = element.serialize
table.pop('ms', None)
return Quadrupole(**table)
ring.replace_group(pattern=r'', factory=factory, kinds=['Sextupole'])
# Set linear dipoles
def apply(element:Element) -> None:
element.linear = True
ring.apply(apply, kinds=['Dipole'])
# Insert correctors
for name, *_ in ring.layout():
if name.startswith('CH'):
corrector = Corrector(f'{name}_CXY', factor=1)
ring.split((1 + 1, None, [name], None), paste=[corrector])
# Merge drifts
ring.merge()
# Change lattice start start
ring.start = "BPM_S01_01"
# Split BPMs
ring.split((None, ['BPM'], None, None))
# Roll lattice
ring.roll(1)
# Splice
ring.splice()
# Describe
ring.describe
[4]:
{'BPM': 168,
'Drift': 732,
'Dipole': 156,
'Quadrupole': 360,
'Corrector': 24,
'Marker': 12}
[5]:
# Compute tunes (fractional part)
nux, nuy = tune(ring, [], matched=True, limit=1)
[6]:
# Compute dispersion
orbit = torch.tensor(4*[0.0], dtype=dtype)
etaqx, etapx, etaqy, etapy = dispersion(ring, orbit, [], limit=1)
[7]:
# Compute twiss parameters
ax, bx, ay, by = twiss(ring, [], matched=True, advance=True, full=False).T
[8]:
# Compute phase advances
mux, muy = advance(ring, [], alignment=False, matched=True).T
[9]:
# Compute coupling
c = coupling(ring, [])
[10]:
# Quadrupole names for global tune correction
QF = [f'QF_S{i:02}_{j:02}' for j in [2, 3] for i in range(1, 12 + 1)]
QD = [f'QD_S{i:02}_{j:02}' for j in [2, 3] for i in range(1, 12 + 1)]
[11]:
# Several local knobs can be used to correct ID effects
# Normal quadrupole correctors
nkn = ['OCT_S01_02', 'QF_S01_02', 'QD_S01_02', 'QD_S01_03', 'QF_S01_03', 'OCT_S01_03']
# Skew quadrupole correctors
nks = ['SD_S01_05', 'SH_S01_02', 'SH_S01_03', 'SD_S01_06']
[12]:
# Define knobs to magnets mixing matrices
Sn = torch.tensor([[1.0, 0.0, 0.0], [0.0, 1.0, 0.0], [0.0, 0.0, 1.0], [0.0, 0.0, 1.0], [0.0, 1.0, 0.0], [1.0, 0.0, 0.0]], dtype=dtype)
print(Sn)
print()
Ss = torch.tensor([[+1.0, 0.0], [0.0, +1.0], [0.0, -1.0], [-1.0, 0.0]], dtype=dtype)
print(Ss)
print()
tensor([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.],
[0., 0., 1.],
[0., 1., 0.],
[1., 0., 0.]], dtype=torch.float64)
tensor([[ 1., 0.],
[ 0., 1.],
[ 0., -1.],
[-1., 0.]], dtype=torch.float64)
[13]:
# Define observables for 'mixed' knobs
def knobs_split(knobs):
kf, kd, kn, ks = torch.split(knobs, [1, 1, 3, 2])
kn = Sn @ kn
ks = Ss @ ks
return kf.squeeze(), kd.squeeze(), kn, ks
def knobs_build(knobs):
kf, kd, kn, ks = knobs_split(knobs)
names = QF + QD
values = torch.stack(len(QF)*[kf] + len(QD)*[kd])
data = {name: value for name, value in zip(names, values)}
for name, value in zip(nkn, kn):
if name in data:
data[name] = data[name] + value
data = {**data, **{name: value for name, value in zip(nkn, kn) if name not in names}}
nn = [name for name in data]
kn = torch.stack([data[name] for name in data])
return (nn, kn), (nks, ks)
def observable_orm(nn, kn, ns, ks):
orm = ORM(ring, orbit, [kn, ks], ('kn', None, nn, None), ('ks', None, ns, None), limit=1)
return orm
def observable(knobs):
(nn, kn), (ns, ks) = knobs_build(knobs)
orm = observable_orm(nn, kn, ns, ks)
return orm.flatten()
[14]:
# Compute target vector and corresponding responce matrix
knobs = torch.tensor((1 + 1 + 3 + 2)*[0.0], dtype=dtype)
target = observable(knobs)
matrix = torch.func.jacfwd(observable)(knobs)
print(knobs.shape)
print(target.shape)
print(matrix.shape)
print(torch.linalg.matrix_rank(matrix))
torch.Size([7])
torch.Size([16128])
torch.Size([16128, 7])
tensor(7)
[15]:
# Define ID model
# Note, only the flattened triangular part of the A and B matrices is passed
A = torch.tensor([[-0.03484222052711237, 1.0272120741819959E-7, -4.698931299341201E-9, 0.0015923185492594811],
[1.0272120579834892E-7, -0.046082787920135176, 0.0017792061173117564, 3.3551298301095784E-8],
[-4.6989312853101E-9, 0.0017792061173117072, 0.056853750760983084, -1.5929605363332683E-7],
[0.0015923185492594336, 3.3551298348653296E-8, -1.5929605261642905E-7, 0.08311631737263032]], dtype=dtype)
B = torch.tensor([[0.03649353186115209, 0.0015448347221877217, 0.00002719892025520868, -0.0033681183134964482],
[0.0015448347221877217, 0.13683886657005795, -0.0033198692682377406, 0.00006140578258682469],
[0.00002719892025520868, -0.0033198692682377406, -0.05260095308967722, 0.005019907688182885],
[-0.0033681183134964482, 0.00006140578258682469, 0.005019907688182885, -0.2531573249456863]], dtype=dtype)
ID = Matrix('ID',
length=0.0,
A=A[torch.triu(torch.ones_like(A, dtype=torch.bool))].tolist(),
B=B[torch.triu(torch.ones_like(B, dtype=torch.bool))].tolist())
[16]:
# Insert ID into the existing lattice
# This will replace the target marker
error = ring.clone()
error.flatten()
error.insert(ID, 'MLL_S01', position=0.0)
error.splice()
# Describe
error.describe
[16]:
{'BPM': 168,
'Drift': 732,
'Dipole': 156,
'Quadrupole': 360,
'Corrector': 24,
'Matrix': 1,
'Marker': 11}
[17]:
# Compute tunes (fractional part)
nux_id, nuy_id = tune(error, [], matched=True, limit=1)
[18]:
# Compute dispersion
orbit = torch.tensor(4*[0.0], dtype=dtype)
etaqx_id, etapx_id, etaqy_id, etapy_id = dispersion(error, orbit, [], limit=1)
[19]:
# Compute twiss parameters
ax_id, bx_id, ay_id, by_id = twiss(error, [], matched=True, advance=True, full=False).T
[20]:
# Compute phase advances
mux_id, muy_id = advance(error, [], alignment=False, matched=True).T
[21]:
# Compute coupling
c_id = coupling(error, [])
[22]:
# Tune shifts
print((nux - nux_id))
print((nuy - nuy_id))
tensor(0.0260, dtype=torch.float64)
tensor(-0.0114, dtype=torch.float64)
[23]:
# Coupling (minimal tune distance)
print(c)
print(c_id)
tensor(0., dtype=torch.float64)
tensor(0.0004, dtype=torch.float64)
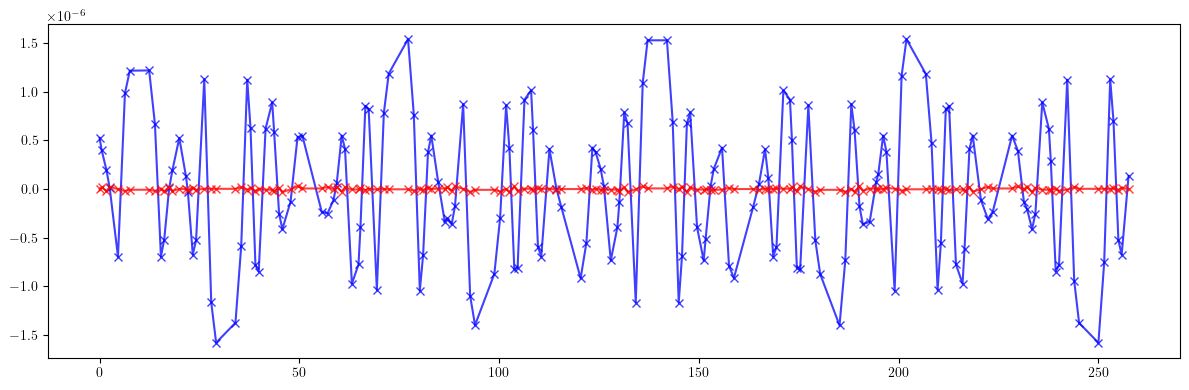
[24]:
# Dispersion
plt.figure(figsize=(12, 4))
plt.errorbar(ring.locations().cpu().numpy(), (etaqx - etaqx_id).cpu().numpy(), fmt='-', marker='x', color='blue', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), (etaqy - etaqy_id).cpu().numpy(), fmt='-', marker='x', color='red', alpha=0.75)
plt.tight_layout()
plt.show()
[25]:
# Beta-beating
plt.figure(figsize=(12, 4))
plt.errorbar(ring.locations().cpu().numpy(), 100*((bx - bx_id)/bx).cpu().numpy(), fmt='-', marker='x', color='blue', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), 100*((by - by_id)/by).cpu().numpy(), fmt='-', marker='x', color='red', alpha=0.75)
plt.tight_layout()
plt.show()
print(100*(((bx - bx_id)/bx)**2).mean().sqrt())
print(100*(((by - by_id)/by)**2).mean().sqrt())
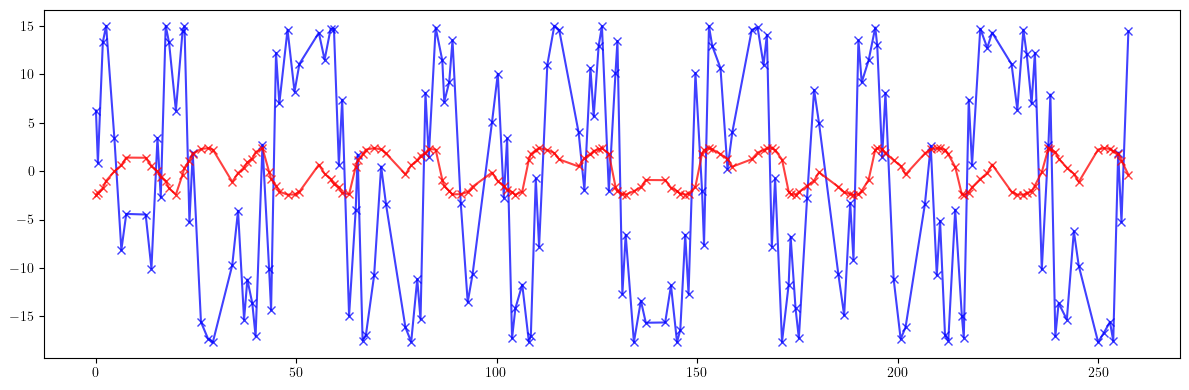
tensor(11.5994, dtype=torch.float64)
tensor(1.7916, dtype=torch.float64)
[26]:
# Phase advance
plt.figure(figsize=(12, 4))
plt.errorbar(ring.locations().cpu().numpy(), 100*((mux - mux_id)/mux).cpu().numpy(), fmt='-', marker='x', color='blue', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), 100*((muy - muy_id)/muy).cpu().numpy(), fmt='-', marker='x', color='red', alpha=0.75)
plt.tight_layout()
plt.show()
print(100*(((mux - mux_id)/mux)**2).mean().sqrt())
print(100*(((muy - muy_id)/muy)**2).mean().sqrt())
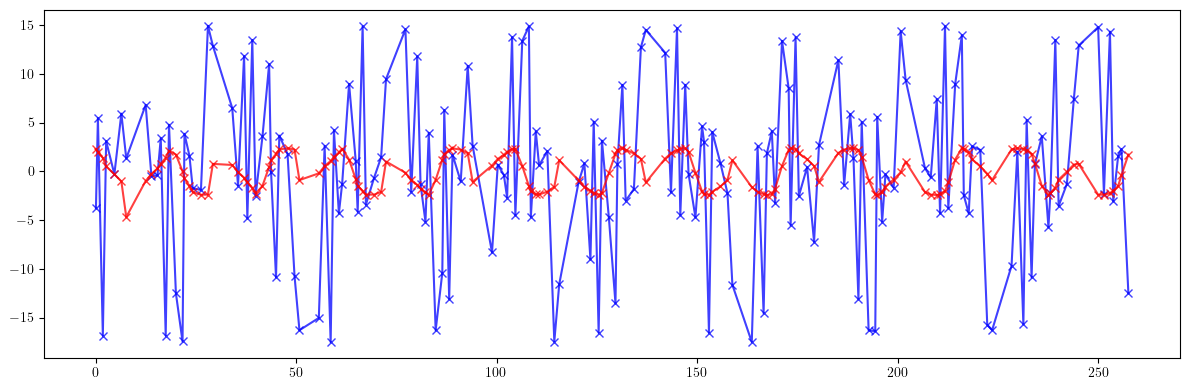
tensor(8.7941, dtype=torch.float64)
tensor(1.7778, dtype=torch.float64)
[27]:
# Define parametric observable vector (emulate tune measurement)
def observable_orm(nn, kn, ns, ks):
orm = ORM(error, orbit, [kn, ks], ('kn', None, nn, None), ('ks', None, ns, None), limit=1)
return orm
def observable(knobs):
(nn, kn), (ns, ks) = knobs_build(knobs)
orm = observable_orm(nn, kn, ns, ks)
return orm.flatten()
[28]:
# Check the residual vector norm
knobs = torch.tensor((1 + 1 + 3 + 2)*[0.0], dtype=dtype)
print(((observable(knobs) - target)**2).sum())
tensor(1498.9104, dtype=torch.float64)
[29]:
# Optimization loop (model free)
# Responce matrix (jacobian)
M = matrix.clone()
# Weighting covariance (sensitivity) matrix
epsilon = 1.0E-9
C = M @ M.T
C = C + epsilon*torch.eye(len(C), dtype=dtype)
# Cholesky decomposition
L = torch.linalg.cholesky(C) # (n_obs, n_obs)
# Whiten response
M = torch.linalg.solve_triangular(L, M, upper=False)
# Additional weights
# Can be used to extra weight selected observables, e.g. tunes
weights = torch.ones(len(M), dtype=dtype)
weights = weights.sqrt()
# Whiten response with additional weights
M = M*weights.unsqueeze(1)
# Number of observables and knobs
n, m = M.shape
# Knob regularization
# Do not use first two knobs (global tune control)
sigma = torch.ones(m, dtype=dtype)
sigma[0] = 0.1
sigma[1] = 0.1
factor = 0.01
S = torch.diag(1.0/sigma**2)
# Augmented matrix
M = torch.cat([M, (factor**0.5)*S], dim=0)
zero = torch.zeros(m, dtype=dtype)
# Iterative correction
lr = 0.75
# Initial value
knobs = torch.tensor((1 + 1 + 3 + 2)*[0.0], dtype=dtype)
for _ in range(16):
value = observable(knobs)
residual = target - value
residual = torch.linalg.solve_triangular(L, residual.unsqueeze(-1), upper=False).squeeze(-1)
residual = weights*residual
residual = torch.cat([residual, zero])
delta = torch.linalg.lstsq(M, residual, driver="gels").solution
knobs += lr * delta
print(((value - target) ** 2).sum())
print()
tensor(1498.9104, dtype=torch.float64)
tensor(120.8736, dtype=torch.float64)
tensor(47.2661, dtype=torch.float64)
tensor(28.0843, dtype=torch.float64)
tensor(21.5719, dtype=torch.float64)
tensor(19.4074, dtype=torch.float64)
tensor(18.7107, dtype=torch.float64)
tensor(18.5113, dtype=torch.float64)
tensor(18.4832, dtype=torch.float64)
tensor(18.5145, dtype=torch.float64)
tensor(18.5662, dtype=torch.float64)
tensor(18.6247, dtype=torch.float64)
tensor(18.6856, dtype=torch.float64)
tensor(18.7473, dtype=torch.float64)
tensor(18.8092, dtype=torch.float64)
tensor(18.8711, dtype=torch.float64)
[30]:
# Apply final corrections
(nn, kn), (ns, ks) = knobs_build(knobs)
result = error.clone()
result.flatten()
for name, knob in zip(nn, kn):
result[name].kn = (result[name].kn + knob).item()
for name, knob in zip(ns, ks):
result[name].ks = (result[name].ks + knob).item()
result.splice()
[31]:
# Compute tunes (fractional part)
nux_result, nuy_result = tune(result, [], matched=True, limit=1)
[32]:
# Compute dispersion
orbit = torch.tensor(4*[0.0], dtype=dtype)
etaqx_result, etapx_result, etaqy_result, etapy_result = dispersion(result, orbit, [], limit=1)
[33]:
# Compute twiss parameters
ax_result, bx_result, ay_result, by_result = twiss(result, [], matched=True, advance=True, full=False).T
[34]:
# Compute phase advances
mux_result, muy_result = advance(result, [], alignment=False, matched=True).T
[35]:
# Compute coupling
c_result = coupling(result, [])
[36]:
# Tune shifts
print((nux - nux_id).abs())
print((nuy - nuy_id).abs())
print()
print((nux - nux_result).abs())
print((nuy - nuy_result).abs())
print()
tensor(0.0260, dtype=torch.float64)
tensor(0.0114, dtype=torch.float64)
tensor(0.0009, dtype=torch.float64)
tensor(0.0012, dtype=torch.float64)
[37]:
# Coupling (minimal tune distance)
print(c)
print(c_id)
print(c_result)
tensor(0., dtype=torch.float64)
tensor(0.0004, dtype=torch.float64)
tensor(7.6666e-06, dtype=torch.float64)
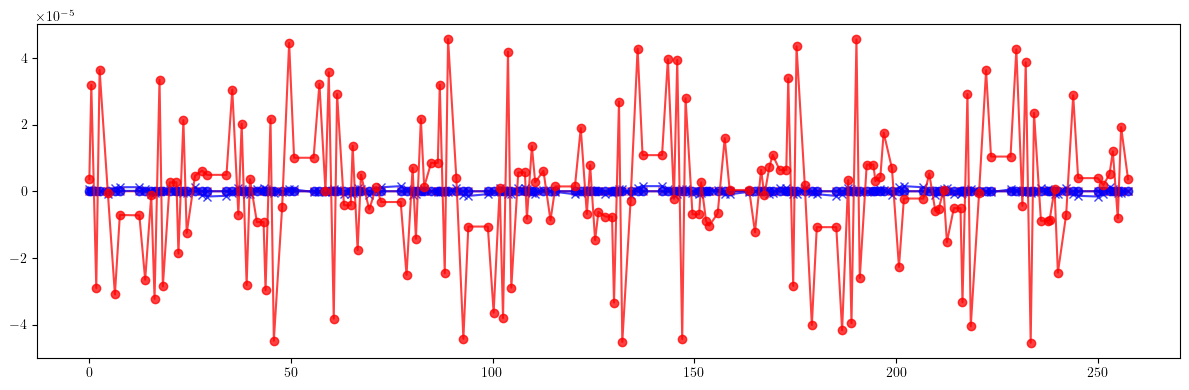
[38]:
# Dispersion
plt.figure(figsize=(12, 4))
plt.errorbar(ring.locations().cpu().numpy(), (etaqx - etaqx_id).cpu().numpy(), fmt='-', marker='x', color='blue', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), (etaqy - etaqy_id).cpu().numpy(), fmt='-', marker='x', color='red', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), (etaqx - etaqx_result).cpu().numpy(), fmt='-', marker='o', color='blue', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), (etaqy - etaqy_result).cpu().numpy(), fmt='-', marker='o', color='red', alpha=0.75)
plt.tight_layout()
plt.show()
[39]:
# Beta-beating
plt.figure(figsize=(12, 4))
plt.errorbar(ring.locations().cpu().numpy(), 100*((bx - bx_id)/bx).cpu().numpy(), fmt='-', marker='x', color='blue', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), 100*((by - by_id)/by).cpu().numpy(), fmt='-', marker='x', color='red', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), 100*((bx - bx_result)/bx).cpu().numpy(), fmt='-', marker='o', color='blue', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), 100*((by - by_result)/by).cpu().numpy(), fmt='-', marker='o', color='red', alpha=0.75)
plt.tight_layout()
plt.show()
print(100*(((bx - bx_id)/bx)**2).mean().sqrt())
print(100*(((by - by_id)/by)**2).mean().sqrt())
print()
print(100*(((bx - bx_result)/bx)**2).mean().sqrt())
print(100*(((by - by_result)/by)**2).mean().sqrt())
print()
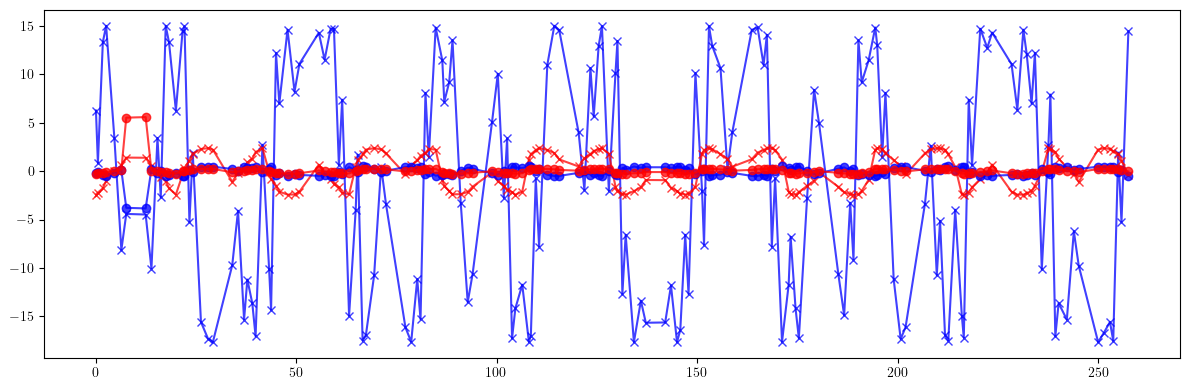
tensor(11.5994, dtype=torch.float64)
tensor(1.7916, dtype=torch.float64)
tensor(0.5372, dtype=torch.float64)
tensor(0.6336, dtype=torch.float64)
[40]:
# Phase advance
plt.figure(figsize=(12, 4))
plt.errorbar(ring.locations().cpu().numpy(), 100*((mux - mux_id)/mux).cpu().numpy(), fmt='-', marker='x', color='blue', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), 100*((muy - muy_id)/muy).cpu().numpy(), fmt='-', marker='x', color='red', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), 100*((mux - mux_result)/mux).cpu().numpy(), fmt='-', marker='o', color='blue', alpha=0.75)
plt.errorbar(ring.locations().cpu().numpy(), 100*((muy - muy_result)/muy).cpu().numpy(), fmt='-', marker='o', color='red', alpha=0.75)
plt.tight_layout()
plt.show()
print(100*(((mux - mux_id)/mux)**2).mean().sqrt())
print(100*(((muy - muy_id)/muy)**2).mean().sqrt())
print()
print(100*(((mux - mux_result)/mux)**2).mean().sqrt())
print(100*(((muy - muy_result)/muy)**2).mean().sqrt())
print()
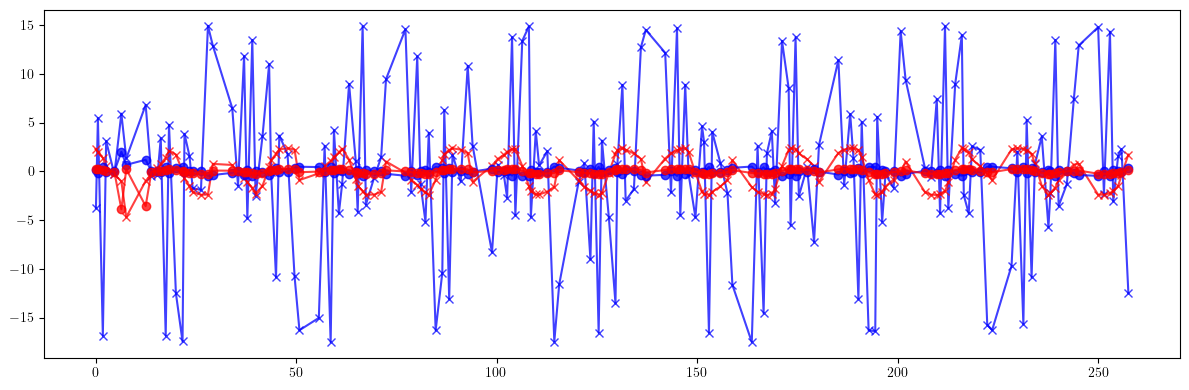
tensor(8.7941, dtype=torch.float64)
tensor(1.7778, dtype=torch.float64)
tensor(0.3195, dtype=torch.float64)
tensor(0.4454, dtype=torch.float64)
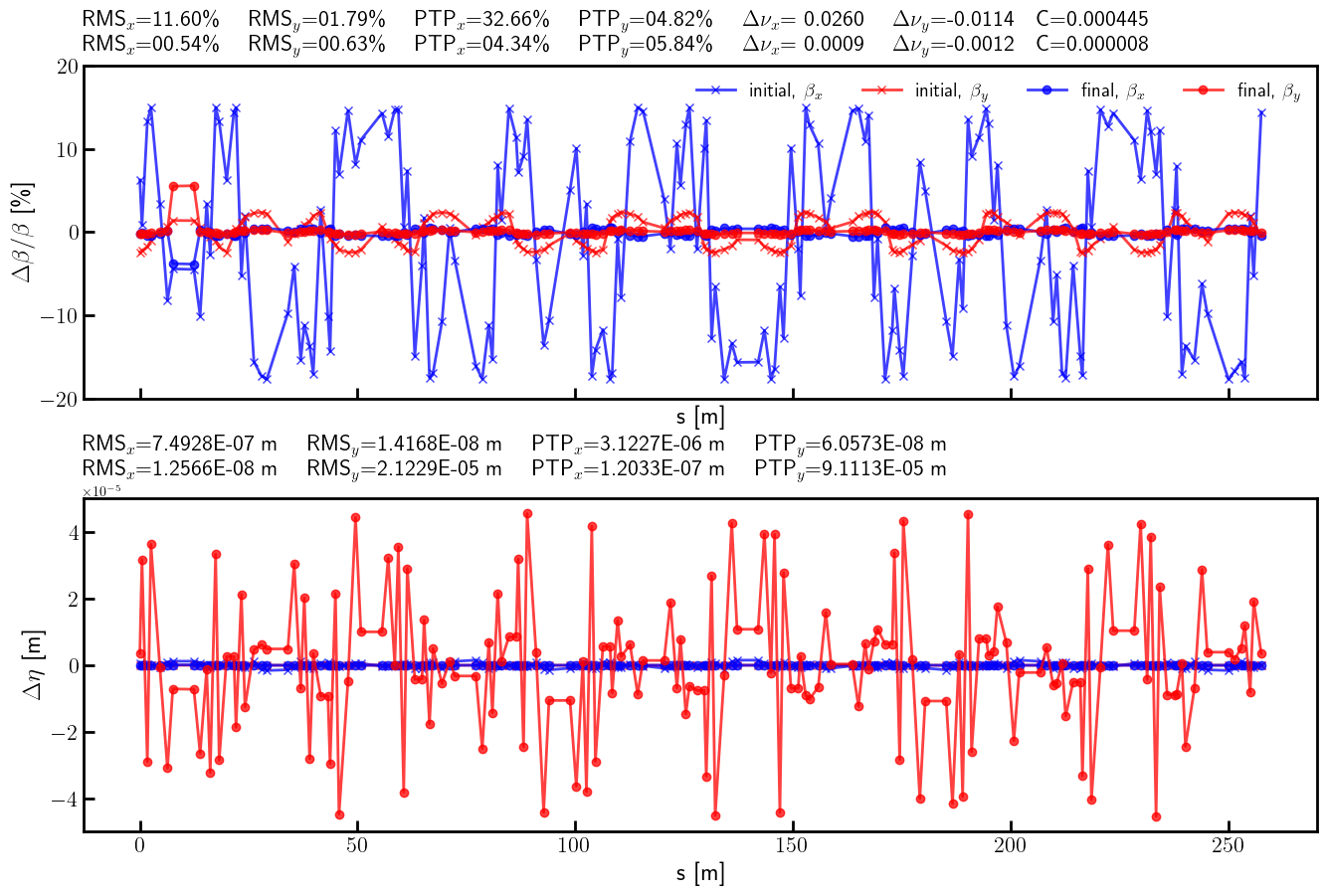
[41]:
# Beta-beating and dispersion
bx_ref_bb = 100.0*(bx - bx_id) / bx
by_ref_bb = 100.0*(by - by_id) / by
bx_res_bb = 100.0*(bx - bx_result)/ bx
by_res_bb = 100.0*(by - by_result)/ by
def rms(x):
return (x**2).mean().sqrt()
rms_x_ref = rms(bx_ref_bb).item()
ptp_x_ref = (bx_ref_bb.max() - bx_ref_bb.min()).item()
rms_y_ref = rms(by_ref_bb).item()
ptp_y_ref = (by_ref_bb.max() - by_ref_bb.min()).item()
rms_x_res = rms(bx_res_bb).item()
ptp_x_res = (bx_res_bb.max() - bx_res_bb.min()).item()
rms_y_res = rms(by_res_bb).item()
ptp_y_res = (by_res_bb.max() - by_res_bb.min()).item()
s = ring.locations().cpu().numpy()
bx_ref_np = bx_ref_bb.cpu().numpy()
by_ref_np = by_ref_bb.cpu().numpy()
bx_res_np = bx_res_bb.cpu().numpy()
by_res_np = by_res_bb.cpu().numpy()
etax_ref = etaqx - etaqx_id
etay_ref = etaqy - etaqy_id
etax_res = etaqx - etaqx_result
etay_res = etaqy - etaqy_result
rms_etax_ref = rms(etax_ref).item()
ptp_etax_ref = (etax_ref.max() - etax_ref.min()).item()
rms_etay_ref = rms(etay_ref).item()
ptp_etay_ref = (etay_ref.max() - etay_ref.min()).item()
rms_etax_res = rms(etax_res).item()
ptp_etax_res = (etax_res.max() - etax_res.min()).item()
rms_etay_res = rms(etay_res).item()
ptp_etay_res = (etay_res.max() - etay_res.min()).item()
etax_ref_np = etax_ref.cpu().numpy()
etay_ref_np = etay_ref.cpu().numpy()
etax_res_np = etax_res.cpu().numpy()
etay_res_np = etay_res.cpu().numpy()
fig, (ax, ay) = plt.subplots(
2, 1, figsize=(16, 10),
sharex=True,
gridspec_kw={'hspace': 0.3}
)
ax.errorbar(s, bx_ref_np, fmt='-', marker='x', color='blue', alpha=0.75, lw=2.0, label=r'initial, $\beta_x$')
ax.errorbar(s, by_ref_np, fmt='-', marker='x', color='red', alpha=0.75, lw=2.0, label=r'initial, $\beta_y$')
ax.errorbar(s, bx_res_np, fmt='-', marker='o', color='blue', alpha=0.75, lw=2.0, label=r'final, $\beta_x$')
ax.errorbar(s, by_res_np, fmt='-', marker='o', color='red', alpha=0.75, lw=2.0, label=r'final, $\beta_y$')
ax.set_xlabel('s [m]', fontsize=18)
ax.set_ylabel(r'$\Delta \beta / \beta$ [\%]', fontsize=18)
ax.tick_params(width=2, labelsize=16)
ax.tick_params(axis='x', length=8, direction='in')
ax.tick_params(axis='y', length=8, direction='in')
title = (
rf'RMS$_x$={rms_x_ref:05.2f}\% \quad RMS$_y$={rms_y_ref:05.2f}\% \quad '
rf'PTP$_x$={ptp_x_ref:05.2f}\% \quad PTP$_y$={ptp_y_ref:05.2f}\% \quad '
rf'$\Delta \nu_x$={(lambda x: '-' if x < 0 else '~')(nux - nux_id)}{(nux - nux_id).abs().item():.4f} \quad $\Delta \nu_y$={(lambda x: '-' if x < 0 else '~')(nuy - nuy_id)}{(nuy - nuy_id).abs().item():.4f}'
rf'\quad C={c_id.item():.6f}'
)
ax.text(0.0, 1.10, title, transform=ax.transAxes, ha='left', va='bottom', fontsize=16, fontfamily='monospace')
title = (
rf'RMS$_x$={rms_x_res:05.2f}\% \quad RMS$_y$={rms_y_res:05.2f}\% \quad '
rf'PTP$_x$={ptp_x_res:05.2f}\% \quad PTP$_y$={ptp_y_res:05.2f}\% \quad '
rf'$\Delta \nu_x$={(lambda x: '-' if x < 0 else '~')(nux - nux_result)}{(nux - nux_result).abs().item():.4f} \quad $\Delta \nu_y$={(lambda x: '-' if x < 0 else '~')(nuy - nuy_result)}{(nuy - nuy_result).abs().item():.4f}'
rf'\quad C={c_result.item():.6f}'
)
ax.text(0.0, 1.025, title, transform=ax.transAxes, ha='left', va='bottom', fontsize=16, fontfamily='monospace')
ax.legend(loc='upper right', frameon=False, fontsize=14, ncol=4)
ax.set_ylim(-20, 20)
ay.errorbar(s, etax_ref_np, fmt='-', marker='x', color='blue', alpha=0.75, lw=2.0, label=r'initial, $\eta_x$')
ay.errorbar(s, etay_ref_np, fmt='-', marker='x', color='red', alpha=0.75, lw=2.0, label=r'initial, $\eta_y$')
ay.errorbar(s, etax_res_np, fmt='-', marker='o', color='blue',alpha=0.75, lw=2.0, label=r'final, $\eta_x$')
ay.errorbar(s, etay_res_np, fmt='-', marker='o', color='red', alpha=0.75, lw=2.0, label=r'final, $\eta_y$')
ay.set_xlabel('s [m]', fontsize=18)
ay.set_ylabel(r'$\Delta \eta$ [m]', fontsize=18)
ay.tick_params(width=2, labelsize=16)
ay.tick_params(axis='x', length=8, direction='in')
ay.tick_params(axis='y', length=8, direction='in')
title = (
rf'RMS$_x$={rms_etax_ref:.4E} m \quad RMS$_y$={rms_etay_ref:.4E} m \quad '
rf'PTP$_x$={ptp_etax_ref:.4E} m \quad PTP$_y$={ptp_etay_ref:.4E} m \quad '
)
ay.text(0.0, 1.125, title, transform=ay.transAxes, ha='left', va='bottom', fontsize=16, fontfamily='monospace')
title = (
rf'RMS$_x$={rms_etax_res:.4E} m \quad RMS$_y$={rms_etay_res:.4E} m \quad '
rf'PTP$_x$={ptp_etax_res:.4E} m \quad PTP$_y$={ptp_etay_res:.4E} m \quad '
)
ay.text(0.0, 1.05, title, transform=ay.transAxes, ha='left', va='bottom', fontsize=16, fontfamily='monospace')
plt.setp(ax.spines.values(), linewidth=2.0)
plt.setp(ay.spines.values(), linewidth=2.0)
plt.show()
[42]:
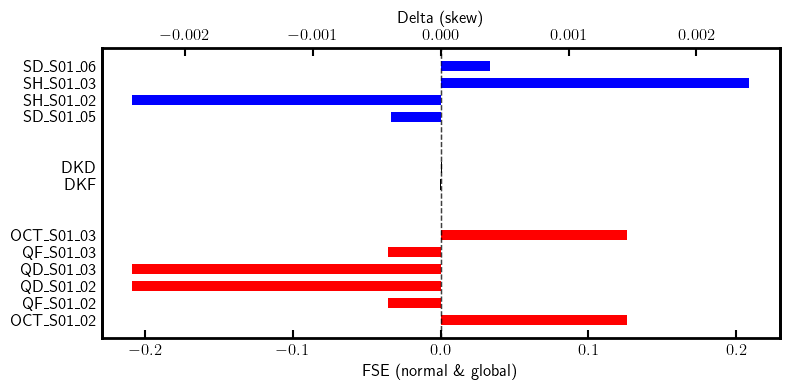
# Knobs
QF = [f'QF_S{i:02}_{j:02}' for j in [2, 3] for i in range(1, 12 + 1)]
QD = [f'QD_S{i:02}_{j:02}' for j in [2, 3] for i in range(1, 12 + 1)]
nkn = ['OCT_S01_02', 'QF_S01_02', 'QD_S01_02', 'QD_S01_03', 'QF_S01_03', 'OCT_S01_03']
nks = ['SD_S01_05', 'SH_S01_02', 'SH_S01_03', 'SD_S01_06']
ring.flatten()
kni = {name: ring[name].kn.item() for name in nkn}
ksi = {name: ring[name].ks.item() for name in nks}
kfi = {name: ring[name].kn.item() for name in QF}
kdi = {name: ring[name].kn.item() for name in QD}
result.flatten()
knf = {name: result[name].kn.item() for name in nkn}
ksf = {name: result[name].ks.item() for name in nks}
kff = {name: result[name].kn.item() for name in QF}
kdf = {name: result[name].kn.item() for name in QD}
print(dkf := [(kff[name] /kfi[name] - 1) for name in kfi if name not in nkn])
print()
print(dkd := [(kdf[name] /kdi[name] - 1) for name in kdi if name not in nkn])
print()
dkf, *_ = dkf
dkd, *_ = dkd
dk = {'DKF': dkf, 'DKD': dkd}
[-5.1480485207089366e-05, -5.1480485207089366e-05, -5.1480485207089366e-05, -5.1480485207089366e-05, -5.1480485207089366e-05, -5.1480485207089366e-05, -5.1480485207089366e-05, -5.1480485207089366e-05, -5.1480485207089366e-05, -5.1480485207089366e-05, -5.1480485207089366e-05, -5.1480485207089366e-05, -5.1480485207089366e-05, -5.1480485207089366e-05, -5.1480485207089366e-05, -5.1480485207089366e-05, -5.1480485207089366e-05, -5.1480485207089366e-05, -5.1480485207089366e-05, -5.1480485207089366e-05, -5.1480485207089366e-05, -5.1480485207089366e-05]
[-0.00018556416673620735, -0.00018556416673620735, -0.00018556416673620735, -0.00018556416673620735, -0.00018556416673620735, -0.00018556416673620735, -0.00018556416673620735, -0.00018556416673620735, -0.00018556416673620735, -0.00018556416673620735, -0.00018556416673620735, -0.00018556416673620735, -0.00018556416673620735, -0.00018556416673620735, -0.00018556416673620735, -0.00018556416673620735, -0.00018556416673620735, -0.00018556416673620735, -0.00018556416673620735, -0.00018556416673620735, -0.00018556416673620735, -0.00018556416673620735]
[43]:
import numpy as np
dkn = np.array([knf[i]/kni[i] - 1 for i in kni])
dks = np.array([ksf[i] - ksi[i] for i in ksi])
n_kn = len(dkn)
n_ks = len(dks)
n_dk = len(dk)
y_kn = np.arange(n_kn)
y_dk = np.arange(n_dk) + n_kn + 2*1
y_ks = np.arange(n_ks) + n_kn + n_dk + 2*2
fig, ax = plt.subplots(figsize=(8, 4))
ay = ax.twiny()
bar_kn = ax.barh(y_kn, dkn, height=0.6, alpha=1, label=r'normal', color='red')
bar_dk = ax.barh(y_dk, list(dk.values()), height=0.6, alpha=1, label=r'global', color='black')
bar_ks = ay.barh(y_ks, dks, height=0.6, alpha=1, label=r'skew', color='blue')
yticks = np.concatenate([y_kn, y_dk, y_ks])
yticklabels = [*kni.keys()] + [*dk.keys()] + [*ksi.keys()]
ax.set_yticks(yticks)
ax.set_yticklabels(yticklabels, fontsize=12)
ay.set_ylim(ax.get_ylim())
ax.axvline(0.0, color='black', linewidth=1.0, linestyle='--', alpha=0.5)
ay.axvline(0.0, color='black', linewidth=1.0, linestyle='--', alpha=0.5)
xmax = max(np.max(np.abs(dkn)), np.max(np.abs(list(dk.values()))))
ax.set_xlim(-1.1 * xmax, 1.1 * xmax)
xmax = np.max(np.abs(dks))
ay.set_xlim(-1.1 * xmax, 1.1 * xmax)
ax.tick_params(axis='x', length=6, width=1.5, direction='in', labelsize=12, bottom=True, top=False, labelbottom=True, labeltop=False)
ax.tick_params(axis='y', length=0, width=0, labelsize=12)
ay.tick_params(axis='x', length=6, width=1.5, direction='in', labelsize=12, bottom=False, top=True, labelbottom=False, labeltop=True)
ax.set_xlabel(r'FSE (normal \& global)', fontsize=12)
ay.set_xlabel(r'Delta (skew)', fontsize=12)
plt.setp(ax.spines.values(), linewidth=2.0)
plt.setp(ay.spines.values(), linewidth=2.0)
ax.spines['top'].set_visible(False)
ay.spines['bottom'].set_visible(False)
plt.tight_layout()
plt.show()